题目内容
如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;

(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G, 求AG的长.

(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G, 求AG的长.
(1)证明△AFD≌△EFD得AF=EF(2) (3)
(3)
 (3)
(3)
试题分析:(1)证明:∵ △EBD是由△CBD折叠而得,
∴ED=DC,BE=BC; 1分
∵四边形ABCD是矩形,∴AB=CD,∠BAD=∠BED=90°
∴ED=AB,而∠EFD=∠AFD
∴△AFD≌△EFD
∴AF=EF
(2)设AF=

∵AB=3,BC=BE=4,AF=EF
∴ BF=4-

∵∠BAF=90°
∴

∴
 ∴
∴
∴tan∠ABF=

(3)∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC;
∴AC=
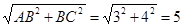 ,
,∴ΔAGF∽ΔCGB
∴

设AG=
 ,则CG=5-
,则CG=5- ,
,∴

解之得:
 ,即AG=
,即AG=
点评:本题考查全等三角形、三角函数,掌握三角函数的定义,会利用三角函数的定义求解,熟悉全等三角形的判定方法

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目





 B.
B. C.
C. D.
D.
 、
、 分别是平行四边形
分别是平行四边形 的边
的边 、
、 上的两点,且
上的两点,且  .
.
 ;
; 是否是平行四边形?
是否是平行四边形?
