题目内容
【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
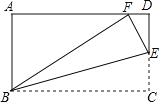
(3)当该函数图象经过点(1,0)时,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小.
【答案】(1) 顶点坐标是(1,4),对称轴为直线x=1;(2) y1>y2.
【解析】分析:(1)将a、b的值代入函数解析式即可;
(2)根据(1)中的结论,即可求得m的值;
(3)根据题意和二次函数的性质,利用分类讨论的数学思想即可求得y1与y2的大小.
详解:(1)当a=-2,b=-4时,
y=-2x2+4x+2=-2(x-1)2+4,
∴该函数图象的顶点坐标是(1,4),对称轴为直线x=1;
(2)点Q(m,t)关于原点对称的点的坐标P是(-m,-t),
则![]() ,
,
解得,m=±1;
(3)∵函数的图象经过点(1,0),
∴0=a-b+2,
∴b=a+2,
∵y=ax2-bx+2,
∴函数的对称轴为直线x=![]() ,
,
当a>0时,![]() <
<![]() +
+![]() <
<![]() +
+![]() ,
,
∵![]() +
+![]() -
-![]() =
=![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=
)=![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y2>y1,
当a<0时,![]() +
+![]() <
<![]() +
+![]() <
<![]() ,
,
∵![]() -(
-(![]() +
+![]() )=-
)=-![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=-
)=-![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y1>y2.

【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表
学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 8 | 13 | a | 10 | 4 |

请你根据统计图表中的信息,解答下列问题:
(1)![]() _______,
_______,![]() _______.
_______.
(2)该调查统计数据的中位数是_______,众数是_______.
(3)请计算扇形统计图中“2次”所对应扇形的圆心角的度数;
(4)若该校共有3000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.