题目内容
如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ= ,则此三角形移动的距离PP′= .
,则此三角形移动的距离PP′= .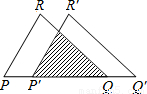
【答案】分析:根据平移的性质知,P′Q′=PQ= ,RQ∥R′Q′,所以S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,即PP′=
,RQ∥R′Q′,所以S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,即PP′= .
.
解答: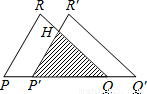 解:由平移的性质知,P′Q′=PQ=
解:由平移的性质知,P′Q′=PQ=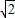 ,RQ∥R′Q′,
,RQ∥R′Q′,
∴△P′QH∽△P′Q′R′
∵S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,
∴P′Q=1,
∴PP′= .
.
故答案为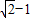 .
.
点评:本题利用了平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
 ,RQ∥R′Q′,所以S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,即PP′=
,RQ∥R′Q′,所以S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,即PP′= .
.解答:
 解:由平移的性质知,P′Q′=PQ=
解:由平移的性质知,P′Q′=PQ=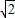 ,RQ∥R′Q′,
,RQ∥R′Q′,∴△P′QH∽△P′Q′R′
∵S△P′QH:S△P′Q′R′=P′Q2:P′Q′2=1:2,
∴P′Q=1,
∴PP′=
 .
.故答案为
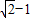 .
.点评:本题利用了平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
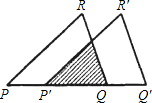 如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=
如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=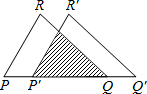 如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=
如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ= ,则此三角形移动的距离PP′= .
,则此三角形移动的距离PP′= .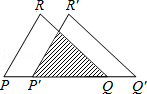
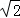 ,则此三角形移动的距离PP′= .
,则此三角形移动的距离PP′= .
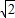 ,则此三角形移动的距离PP′= .
,则此三角形移动的距离PP′= .