Question

如图，已知AB是⊙O的直径，E是AB延长线上的一点，D是⊙O上的一点，且AD平分∠FAE，ED⊥AF交AF的延长线于点C
【小题1】判断直线CE与⊙O的位置关系，并证明你的结论；
【小题2】若AF∶FC=5∶3，AE=16，求⊙O的直径AB的长．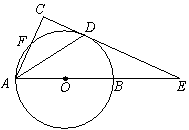

Answer 1

【小题1】直线CE与⊙O相切…………1分
证明：如图，连结 OD
∵AD平分∠FAE， ∴∠CAD=∠DAE．……………2分
∵OA=OD，∴∠ODA=∠DAE．
∴∠CAD=∠ODA∴OD∥AC        ……………3分
∵EC⊥AC，∴OD⊥EC
∴CE是⊙O的切线．……………4分
【小题2】如图，连结BF．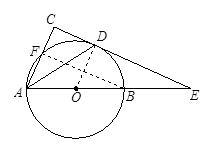

∵ AB是⊙O的直径，
∴ ∠AFB=90°． ……………5分
∵∠C=90°，
∴∠AFB=∠C      ……………6分
∴BF∥EC  ∴AF∶AC= AB∶AE．      ……………7分
∵ AF∶FC=5∶3，AE=16，
∴5∶8=AB∶16． ∴AB= 10．…………………………8分

解析