题目内容
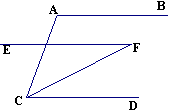
8、如图,已知EF∥CD∥AB,EA∥FB,CD、AF交于G,则图中与△ACG相似的三角形有:
△AEF、△FDG、△FBA
.
分析:由EF∥CD∥AB,EA∥FB,根据平行于三角形一边的直线截三角形另两边或另两边的延长线所得三角形与原三角形相似,即可证得△ACG∽△FDG,△ACG∽△AEF,△FDG∽△FBA,又由相似三角形的传递性,即可求得答案.
解答:解:∵EA∥FB,
∴△ACG∽△FDG,
∵EF∥CD∥AB,
∴△ACG∽△AEF,△FDG∽△FBA,
∴△ACG∽△AEF∽△FDG∽△FBA.
故答案为:△AEF、△FDG、△FBA.
∴△ACG∽△FDG,
∵EF∥CD∥AB,
∴△ACG∽△AEF,△FDG∽△FBA,
∴△ACG∽△AEF∽△FDG∽△FBA.
故答案为:△AEF、△FDG、△FBA.
点评:此题考查了相似三角形的判定定理.此题难度不大,解题的关键是注意平行于三角形一边的直线截三角形另两边或另两边的延长线所得三角形与原三角形相似定理的应用.

练习册系列答案
相关题目
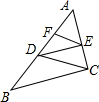 (2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( )
(2012•虹口区一模)如图,已知EF∥CD,DE∥BC,下列结论中不一定正确的是( ) 如图,已知EF⊥CD于F,∠GEF=25°,∠1=65°,则AB与CD平行吗?请说明理由.
如图,已知EF⊥CD于F,∠GEF=25°,∠1=65°,则AB与CD平行吗?请说明理由.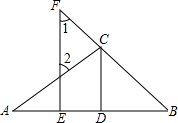 如图,已知EF∥CD,∠1=∠2,请说明CD平分∠ACB的理由.
如图,已知EF∥CD,∠1=∠2,请说明CD平分∠ACB的理由.