题目内容
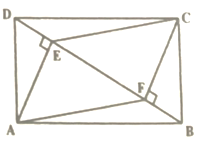
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
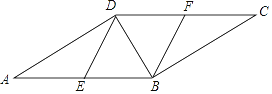
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
【答案】(1)见解析;(2)见解析.
【解析】(1)由平行四边形性质得AD=BC,AB=CD,∠A=∠C,再由E、F分别为边AB、CD的中点,证AE=CF,根据SAS证△ADE≌△CBF.
(2)由DF和BE平行且相等,证四边形EBFD是平行四边形,再根据直角三角形斜边上的中线等于斜边一半,可得BF=DF,所以四边形BEDF是菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE= ![]() AB,CF=
AB,CF= ![]() CD,
CD,
∴AE=CF,
在△ADE和△CBF中,
∵ 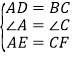 ,
,
∴△ADE≌△CBF(SAS).
(2)证明:∵E、F分别为边AB、CD的中点,
∴DF= ![]() DC,BE=
DC,BE=![]() AB,
AB,
又∵在ABCD中,AB∥CD,AB=CD,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∵DB⊥BC,
∴∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边DC的中点,
∴BF= ![]() DC=DF,
DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
新加入人数(人) | 153 | 550 | 653 | b | 725 |
累计总人数(人) | 3353 | 3903 | a | 5156 | 5881 |
(1)表格中a= ,b= ;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是 (只要填写正确说法前的序号).
①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.