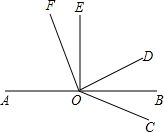
题目内容
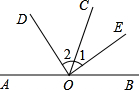 如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
(1)∠BOC=72°20′,求∠1,∠2,∠DOE的度数.
(2)若∠BOC=a,求∠DOE.
解:(1)∵AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
∠BOC=72°20′,
∴∠1=∠EOB= ∠BOC=36°10′,
∠BOC=36°10′,
∴∠DOC=∠AOD= ∠AOC=
∠AOC= (180°-∠BOC)=
(180°-∠BOC)= (180°-72°20′)=53°50′,
(180°-72°20′)=53°50′,
∴∠DOE=∠1+∠2=36°10′+53°50′=90°;
(2)∵AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
∴∠DOE= ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ×180°=90°.
×180°=90°.
分析:(1)根据角平分线的性质得出∠1=∠EOB= ∠BOC,以及∠DOC=∠AOD=
∠BOC,以及∠DOC=∠AOD= ∠AOC和平角的定义分别求出即可,进而求出∠DOE的度数;
∠AOC和平角的定义分别求出即可,进而求出∠DOE的度数;
(2)根据角平分线的性质得出∠DOE= ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)即可得出答案.
(∠AOC+∠BOC)即可得出答案.
点评:此题主要考查了角的有关计算,熟练地应用角平分线的性质得出角之间的关系是解题关键.
∠BOC=72°20′,
∴∠1=∠EOB=
 ∠BOC=36°10′,
∠BOC=36°10′,∴∠DOC=∠AOD=
 ∠AOC=
∠AOC= (180°-∠BOC)=
(180°-∠BOC)= (180°-72°20′)=53°50′,
(180°-72°20′)=53°50′,∴∠DOE=∠1+∠2=36°10′+53°50′=90°;
(2)∵AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
∴∠DOE=
 ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ×180°=90°.
×180°=90°.分析:(1)根据角平分线的性质得出∠1=∠EOB=
 ∠BOC,以及∠DOC=∠AOD=
∠BOC,以及∠DOC=∠AOD= ∠AOC和平角的定义分别求出即可,进而求出∠DOE的度数;
∠AOC和平角的定义分别求出即可,进而求出∠DOE的度数;(2)根据角平分线的性质得出∠DOE=
 ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)即可得出答案.
(∠AOC+∠BOC)即可得出答案.点评:此题主要考查了角的有关计算,熟练地应用角平分线的性质得出角之间的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
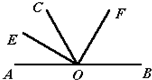 24、如图,AB是直线,OE、OF分别是∠AOC和∠BOC的平分线.
24、如图,AB是直线,OE、OF分别是∠AOC和∠BOC的平分线.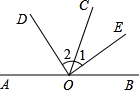 如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.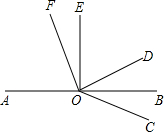 如图,AB是直线,O是AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC,则图中与∠DOE互余的角有
如图,AB是直线,O是AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC,则图中与∠DOE互余的角有