题目内容
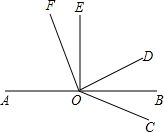
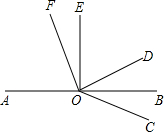 如图,AB是直线,O是AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC,则图中与∠DOE互余的角有
如图,AB是直线,O是AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC,则图中与∠DOE互余的角有3
3
个;与∠DOE互补的角有2
2
个.分析:由∠AOE=90°,可得∠BOE=90°,则∠DOE+∠BOD=90°,要求与∠DOE互余的角,只要找到与∠BOD相等的角即可,即∠BOC,∠EOF;根据同角的补角相等,可得∠DOE=∠AOF,则∠DOE的补角与∠AOF的补角相等,即∠DOE互补的角:∠BOF、∠EOC.
解答:解:∵∠AOE=∠FOD=90°,
∴∠AOF+∠EOF=90°,∠BOD+∠DOE=90°,∠DOE+∠EOF=90°,
∵OB平分∠COD,
∴∠BOD=∠BOC,
∴∠DOE互余的是∠EOF、∠BOD、∠BOC,共3个.
∵∠AOF+∠BOF=180°,∠DOE+∠BOF=180°,
∴与∠DOE互补的角是∠BOF、∠EOC,共2个.
故答案为:3,2.
∴∠AOF+∠EOF=90°,∠BOD+∠DOE=90°,∠DOE+∠EOF=90°,
∵OB平分∠COD,
∴∠BOD=∠BOC,
∴∠DOE互余的是∠EOF、∠BOD、∠BOC,共3个.
∵∠AOF+∠BOF=180°,∠DOE+∠BOF=180°,
∴与∠DOE互补的角是∠BOF、∠EOC,共2个.
故答案为:3,2.
点评:本题考查了补角和余角的定义,性质:同角或等角的余角相等,同角或等角的补角相等.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
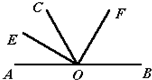 24、如图,AB是直线,OE、OF分别是∠AOC和∠BOC的平分线.
24、如图,AB是直线,OE、OF分别是∠AOC和∠BOC的平分线.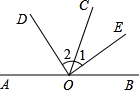 如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.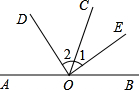 如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.
如图,AB是直线,OD,OE分别是∠AOC,∠BOC的平分线.