题目内容
【题目】正方形ABCD的边长为2,M、N分别为边BC、CD上的动点,且∠MAN=45°
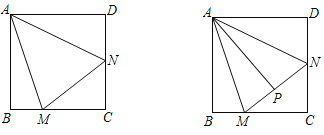
(1)猜想线段BM、DN、MN的数量关系并证明;
(2)若BM=CM,P是MN的中点,求AP的长;
(3)M、N运动过程中,请直接写出△AMN面积的最大值 和最小值 .
【答案】(1)BM+DN=MN;(2)![]() ;(3)2,4
;(3)2,4![]() ﹣4.
﹣4.
【解析】
(1)延长CB到E,使BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出AE=AN,∠DAN=∠BAE,求出∠NAM=∠MAE,根据SAS证出△NAM≌△EAM,从而得到BM+DN=MN;
(2)如图2,过点A作AF⊥MN,由AAS可证△ABM≌△AFM,可得AB=AF=2,MB=MF=1,由勾股定理可求DN=![]() ,即可求PF的长,由勾股定理可求AP的长;(3)由三角形的面积公式可求△AMN面积=MN,由三角形的三边关系和完全平方公式可求MN的最大值和最小值,即可求解.
,即可求PF的长,由勾股定理可求AP的长;(3)由三角形的面积公式可求△AMN面积=MN,由三角形的三边关系和完全平方公式可求MN的最大值和最小值,即可求解.
解:
(1)BM+DN=MN.
理由:如图,延长CB至E使得BE=DN,连接AE,
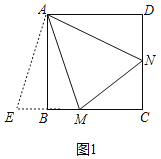
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中,
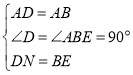 ,
,
∴△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中,
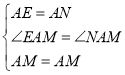 ,
,
∴△EAM≌△NAM(SAS),
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN.
(2)如图2,过点A作AF⊥MN,

∵点M是BC的中点,
∴BM=MC=![]() BC=1,
BC=1,
由(1)可知:∠AMB=∠AMF,∠ABM=∠AFM=90°,AM=AM,
∴△ABM≌△AFM(AAS),
∴AB=AF=2,MB=MF=1,
∵BM+DN=MN,
∴DN=NF,
∵MC2+NC2=MN2,
∴1+(2﹣DN)2=(1+DN)2,
∴DN=![]() ,
,
∴MN=1+DN=![]() ,
,
∵P是MN的中点,
∴MP=![]() ,
,
∴PF=MF﹣MP=![]() ,
,
∴AP=![]() .
.
(3)∵△AMN面积=![]() MN×AF,
MN×AF,
∴△AMN面积=MN,
∵MN=BM+DN,BM+CM=BC=2,DN+CN=CD=2,
∴MN+CM+CN=BC+CD=4,
∴CM+CN=4﹣MN,
∴2CMCN+CM2+CN2=(4﹣MN)2=16+MN2﹣8MN,且CM2+CN2=MN2,
∴CMCN=8﹣4MN,
∵(CM﹣CN)2≥0,
∴CM2+CN2≥2CMCN,
∴MN2≥16﹣8MN,
∴(MN+4)2≥32,
∴MN≥![]() ﹣4,或MN≤﹣
﹣4,或MN≤﹣![]() ﹣4(舍去),
﹣4(舍去),
∴MN的最小值为![]() ﹣4,
﹣4,
∴△AMN面积的最小值为![]() ﹣4,
﹣4,
∵MN+CM+CN=4,且CM+CN≤MN,
∴MN≤4﹣MN,
∴MN≤2,
∴MN的最大值为2,
∴△AMN面积的最大值为2;
故答案为2,![]() ﹣4.
﹣4.