题目内容
如图所示①,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF= 。
。
 。
。 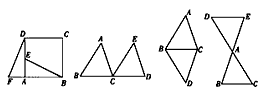
① ② ③ ④
(1)求证:△ABE≌△ADF;
(2)阅读下面材料:
如图②,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;
如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置。
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换。
回答下列问题:
①在图①中,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
②指出图①中线段BE与DF之间的关系。
(2)阅读下面材料:
如图②,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置;
如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置。
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换。
回答下列问题:
①在图①中,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
②指出图①中线段BE与DF之间的关系。
解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠FAD=EAB=90°,
又∵E是AD的中点,
 ,
,
∴AF=AE,
在△ADF 与△ABE中,
AD=AB,∠FAD=∠EAB,AF=AE,
∴△ADF≌△ABE(SAS);
(2)①旋转;②大小相等并且互相垂直。
∴AB=AD,∠FAD=EAB=90°,
又∵E是AD的中点,
 ,
,∴AF=AE,
在△ADF 与△ABE中,
AD=AB,∠FAD=∠EAB,AF=AE,
∴△ADF≌△ABE(SAS);
(2)①旋转;②大小相等并且互相垂直。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
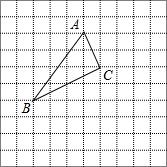 如图所示,△ABC在正方形网格中,若点A的坐标为(0,4),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,4),按要求回答下列问题: 如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: 如图所示,△ABC在正方形网格中,若点A的坐标为(0,5),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,5),按要求回答下列问题: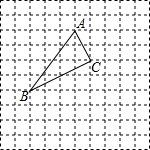 如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: 轴的对称图形△A′B′C′.(不用写作法)
轴的对称图形△A′B′C′.(不用写作法)