题目内容
某工厂现有甲种原料360kg,乙种原料290kg,计划用它们生产A、B两种产品共50件,已知每生产一件A种产品,需要甲种原料9kg、乙种原料3kg,获利700元,生产一件B种产品,需要甲种原料4kg、乙种原料10kg,可获利1200元.
(1)利用这些原料,生产A、B两种产品,有哪几种不同的方案?
(2)设生产两种产品总利润为y(元),其中生产A中产品x(件),试写出y与x之间的函数解析式.
(3)利用函数性质说明,采用(1)中哪种生产方案所获总利润最大?最大利润是多少?
(1)符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;(2)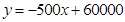 ;(3)第一种方案,45000.
;(3)第一种方案,45000.
解析试题分析:(1)关系式为:A种产品需要甲种原料数量+B种产品需要甲种原料数量≤360;A种产品需要乙种原料数量+B种产品需要乙种原料数量≤290,把相关数值代入即可;解不等式,得到关于x的范围,根据整数解可得相应方案
(2)总获利=700×A种产品数量+1200×B种产品数量;
(3)根据函数的增减性和(1)得到的取值可得最大利润.
试题解析:(1)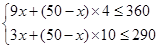 ;解第一个不等式得:
;解第一个不等式得: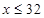 ,解第二个不等式得:
,解第二个不等式得: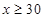 ,∴
,∴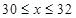 ,∵
,∵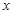 为正整数,∴
为正整数,∴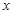 =30、31、32,∴50﹣30=20,50﹣31=19,50﹣32=18,∴符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;
=30、31、32,∴50﹣30=20,50﹣31=19,50﹣32=18,∴符合的生产方案有三种,分别为①生产A产品30件,B产品20件;②生产A产品31件,B产品19件;③生产A产品32件,B产品18件;
(2)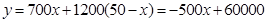 ,
,
(3)∵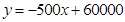 ,﹣500<0,而
,﹣500<0,而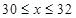 ,∴当
,∴当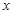 越小时,总利润
越小时,总利润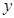 越大,即当
越大,即当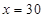 时,最大利润为:
时,最大利润为: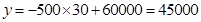 元.∴生产A产品30件,B产品20件使生产A、B两种产品的总获利最大,最大利润是45000元.
元.∴生产A产品30件,B产品20件使生产A、B两种产品的总获利最大,最大利润是45000元.
考点:1.一元一次不等式组的应用;2.方案型.

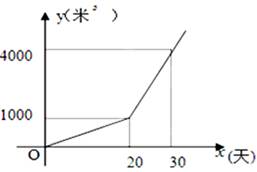
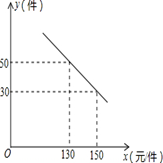
 阅读快车系列答案
阅读快车系列答案 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像.
(时)的函数的部分图像.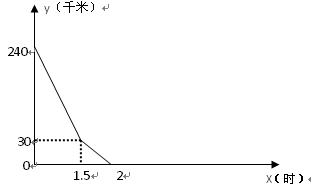
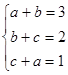 的解满足
的解满足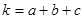 ,求关于
,求关于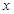 的函数
的函数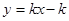 的解析式.
的解析式. :
: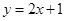 、直线
、直线 :
: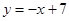 ,直线
,直线
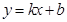 的图象经过点
的图象经过点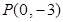 ,且与函数
,且与函数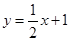 的图象相交于点
的图象相交于点 .
.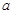 的值;
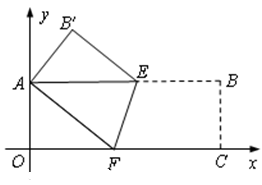
的值;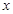 轴的交点是B,函数
轴的交点是B,函数 轴的交点是C,求四边形
轴的交点是C,求四边形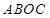 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与 轴围成的三角形的面积.
轴围成的三角形的面积. 