题目内容
给出两个命题:①三角形的一个外角大于任何一个内角;②各边对应成比例的两个矩形一定相似( )
| A.①真②真 | B.①假②真 | C.①真②假 | D.①假②假 |
B
解析试题分析:根据三角形的外角的性质、相似多边形的判定方法依次分析各小题即可作出判断.
解:①三角形的一个外角大于任何一个与它不相邻的内角,所以为假命题;
②各边对应成比例的两个矩形一定相似,为真命题;
故选B.
考点:真假命题
点评:本题属于基础应用题,只需学生熟练掌握平面图形的基本概念,即可完成.

练习册系列答案
相关题目
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=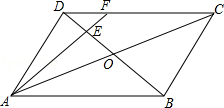
| A.1:4 | B.1:3 | C.2:3 | D.1:2 |
如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为
A. | B. | C.2 | D.3 |
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为【 】
| A.5cm | B.6cm | C.7cm | D.8cm |

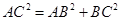 B.
B.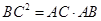 C.
C.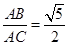 D.
D.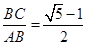
 ,若再增加一个条件就能使结论“
,若再增加一个条件就能使结论“ ”成立,则这个条件可以是____________.(只填一个即可)
”成立,则这个条件可以是____________.(只填一个即可)
 ,则△CEF的周长是 .
,则△CEF的周长是 .

