ЬтФПФкШн
ЁОЬтФПЁПЮЪЬтЬНОПЃК
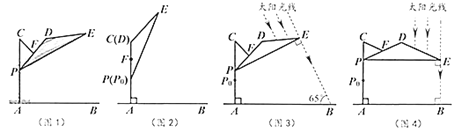
(1)ШчЭМ1,дкЁїABCжа,ЁЯB=90ЃЌAB=3ЃЌBC=4ЃЌШєЁїABCЕФБпЩЯДцдкЕуPЃЌЪЙЁїABPЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЃЌдђCPЕФГЄЮЊ______ЃЛ
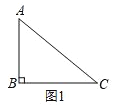
(2)ШчЭМ2,дкОиаЮABCDжа,AB=3,БпBCЩЯДцдкЕуP,ЪЙЁЯAPD=90ЃЌЧѓОиаЮABCDУцЛ§ЕФзюаЁжЕ.
ЮЪЬтНтОіЃК
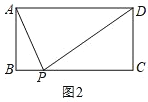
(3)ШчЭМ3,дкЫФБпаЮABCDжа,AB=3,ЁЯA=ЁЯB=90,ЁЯC=45,БпCDЩЯДцдкЕуP,ЪЙЁЯAPB=60ЁуЃЌдкДЫЬѕМўЯТЃЌЫФБпаЮABCDЕФУцЛ§ЪЧЗёДцдкзюДѓжЕ?ШєДцдкЃЌЧѓГізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1) 1Лђ![]() Лђ2ЃЛ(2) ОиаЮABCDУцЛ§ЕФзюаЁжЕЮЊ18ЃЛ(3)ДцдкЃЌ
Лђ2ЃЛ(2) ОиаЮABCDУцЛ§ЕФзюаЁжЕЮЊ18ЃЛ(3)ДцдкЃЌ![]() +
+![]() .
.
ЁОНтЮіЁПЃЈ1ЃЉЗжШ§жжЧщаЮЗжБ№ЧѓНтМДПЩЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБвдADЮЊжБОЖЕФЁбOгыBCЯрЧаЪБЃЌЧаЕуЮЊPЃЌДЫЪБЁЯAPD=90ЁуЃЌADЕФГЄзюаЁЃЎЧѓГіADЕФГЄМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉДцдкЃЎШчЭМ3жаЃЌШчЭМзїЕШБпШ§НЧаЮABMЕФЭтНгдВЁбOЃЌЕБжБЯпCDгыЁбOЯрЧагыPЪБЃЌЫФБпаЮABCDЕФУцЛ§зюДѓЃЌДЫЪБТњзуЬѕМўЁЯAPB=ЁЯAMB=60ЁуЃЎЯыАьЗЈЧѓГіADЁЂABМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМ1жаЃЌзїBHЁЭACЃЎ
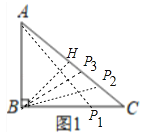
дкRtЁїABCжаЃЌЁпЁЯABC=90ЁуЃЌAB=3ЃЌBC=4ЃЌЁрAC=![]() =5ЃЎ
=5ЃЎ
Ёп![]() ABBC=
ABBC=![]() ACBHЃЌЁрBH=
ACBHЃЌЁрBH=![]() ЃЎдкRtЁїABHжаЃЌAH=
ЃЎдкRtЁїABHжаЃЌAH=![]() =
=![]() ЃЌЗжШ§жжЧщПіЬжТлЃК
ЃЌЗжШ§жжЧщПіЬжТлЃК
ЂйЕБBA=BP1ЪБЃЌPC1=4Љ3=1ЃЎ
ЂкЕБBA=BP2ЪБЃЎЁпBHЁЭAP2ЃЌЁрAH=HP2=![]() ЃЌЁрCP2=ACЉAP2=5Љ
ЃЌЁрCP2=ACЉAP2=5Љ![]() =
=![]() ЃЎ
ЃЎ
ЂлЕБAB=AP3ЪБЃЌCP3=5Љ3=2ЃЎ
злЩЯЫљЪіЃКТњзуЬѕМўЕФPCЕФжЕЮЊ1Лђ![]() Лђ2ЃЎ
Лђ2ЃЎ
ЙЪД№АИЮЊЃК1Лђ![]() Лђ2ЃЎ
Лђ2ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБвдADЮЊжБОЖЕФЁбOгыBCЯрЧаЪБЃЌЧаЕуЮЊPЃЌДЫЪБЁЯAPD=90ЁуЃЌADЕФГЄзюаЁЃЎ

СЌНгOPЃЎдђOPЁЭBCЃЌвзжЄЫФБпаЮBPOЃЌЫФБпаЮCDOPЖМЪЧе§ЗНаЮЃЌЁрBC=AD=6ЃЌAB=CD=3ЃЌЁрОиаЮABCDУцЛ§ЕФзюаЁжЕЮЊ18ЃЎ
ЃЈ3ЃЉДцдкЃЎШчЭМ3жаЃЌШчЭМзїЕШБпШ§НЧаЮABMЕФЭтНгдВЁбOЃЌЕБжБЯпCDгыЁбOЯрЧагыPЪБЃЌЫФБпаЮABCDЕФУцЛ§зюДѓЃЌДЫЪБТњзуЬѕМўЁЯAPB=ЁЯAMB=60ЁуЃЎ
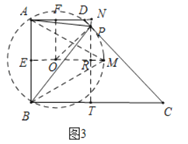
бгГЄMOНЛABгыEЃЌзїOFЁЭADгыFЃЌPTЁЭBCгыTЃЌСЌНгOPЃЎЃЌPTНЛOMгкRЃЎ
ЁпAB=3ЃЌADЁЮBCЃЌЁЯC=45ЁуЃЌЁрCD=![]() AB=3
AB=3![]() ЃЎ
ЃЎ
ЁпЁїABMЪЧЕШБпШ§НЧаЮЃЌЫФБпаЮAEOFЪЧОиаЮЃЌЁрAE=EB=NR=RT=![]() ЃЌAF=EO=
ЃЌAF=EO=![]() ЃЌOM=OP=
ЃЌOM=OP=![]() ЃЌOR=PR=
ЃЌOR=PR=![]() ЃЌЁрBT=AN=
ЃЌЁрBT=AN=![]() +
+![]() ЃЌPN=DN=TNЉPT=3Љ
ЃЌPN=DN=TNЉPT=3Љ![]() Љ
Љ![]() =
=![]() ЃЌЁрAD=ANЉDN=
ЃЌЁрAD=ANЉDN=![]() ЉЃЈ
ЉЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌBC=BT+CT=
ЃЌBC=BT+CT=![]() +
+![]() +
+![]() =
=![]() ЃЌЁрSЫФБпаЮABCD=
ЃЌЁрSЫФБпаЮABCD=![]() AB=
AB=![]() ЃЈ
ЃЈ![]() ЃЉ=
ЃЉ=![]() +3
+3![]() ЃЎ
ЃЎ