题目内容
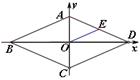
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.

(1)△ADE与△BEC全等吗?请写出必要的推理过程;
(2)若已知AD=6,AB=14,请求出△CED的面积.

(1)△ADE与△BEC全等吗?请写出必要的推理过程;
(2)若已知AD=6,AB=14,请求出△CED的面积.
(1)Rt△ADE≌Rt△BEC;
(2)△CED的面积为:50.
(2)△CED的面积为:50.
试题分析:(1)由∠1=∠2,可得DE=CD,根据证明直角三角形全等的“HL”定理,证明即可;
(2)根据题意,∠AED+∠ADE=90°,∠BEC+∠BCE=90°,又∠AED=∠BCE,∠ADE=∠BEC,所以,∠AED+∠BEC=90°,即可证得∠DEC=90°,即可得出;再由(1)可得BE=AD,所以可求出AE,根据勾股定理可求出DE,再由已知∠1=∠2,从而求出△CED的面积.
点评:证明三角形全等时,关键是根据题意选取适当的条件.

练习册系列答案
相关题目
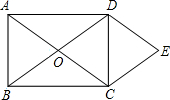
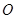 为矩形
为矩形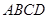 的对角线的交点,
的对角线的交点,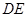 ∥
∥ ,
, ∥
∥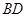 。
。
 的形状,并说明理由;(8分)
的形状,并说明理由;(8分)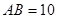 ,
,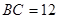 ,求四边形
,求四边形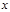 轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(
轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(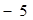 ,
, )和(
)和(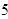 ,
,

 中,
中,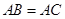 ,
,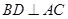 ,
, , 垂足分别为点
, 垂足分别为点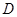 ,
, ,连接
,连接 .试问四边形
.试问四边形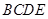 是等腰梯形吗?为什么?
是等腰梯形吗?为什么?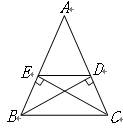
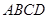 中,
中,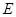 是
是 边上的中点,
边上的中点, 与
与 相交于点
相交于点 ,连接
,连接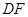 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角). 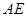 试判断
试判断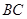 于点
于点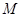 ,试判断
,试判断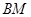 与
与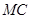 的数量关系,并说明理由.
的数量关系,并说明理由.
