题目内容
 (2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
(2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=| 1 | 2 |
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
分析:(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
解答: (1)证明:在?ABCD中,AD∥BC,且AD=BC.
(1)证明:在?ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=
AD.
又∵CE=
BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在?ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=2,DH=2
.
在?CEDF中,CE=DF=
AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE=
=
.
 (1)证明:在?ABCD中,AD∥BC,且AD=BC.
(1)证明:在?ABCD中,AD∥BC,且AD=BC.∵F是AD的中点,
∴DF=
| 1 |
| 2 |
又∵CE=
| 1 |
| 2 |
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在?ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=2,DH=2
| 3 |
在?CEDF中,CE=DF=
| 1 |
| 2 |
∴在Rt△DHE中,根据勾股定理知DE=
(2
|
| 13 |
点评:本题考查了平行四边形的判定与性质、勾股定理.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
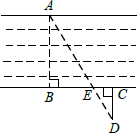 (2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
(2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )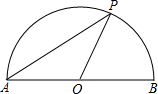 (2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) (2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
(2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=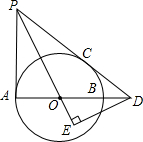 (2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.