题目内容
 (2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
(2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=| 1 |
| x |
-
| 3 |
| 2 |
-
,a2013=| 3 |
| 2 |
-
| 1 |
| 3 |
-
;若要将上述操作无限次地进行下去,则a1不可能取的值是| 1 |
| 3 |
0、-1
0、-1
.分析:求出a2,a3,a4,a5的值,可发现规律,继而得出a2013的值,根据题意可得A1不能在x轴上,也不能在y轴上,从而可得出a1不可能取的值.
解答:解:当a1=2时,B1的纵坐标为
,
B1的纵坐标和A2的纵坐标相同,则A2的横坐标为a2=-
,
A2的横坐标和B2的横坐标相同,则B2的纵坐标为b2=-
,
B2的纵坐标和A3的纵坐标相同,则A3的横坐标为a3=-
,
A3的横坐标和B3的横坐标相同,则B3的纵坐标为b3=-3,
B3的纵坐标和A4的纵坐标相同,则A4的横坐标为a4=2,
A4的横坐标和B4的横坐标相同,则B4的纵坐标为b4=
,
即当a1=2时,a2=-
,a3=-
,a4=2,a5=-
,
b1=
,b2=-
,b3=-3,b4=
,b5=-
,
∵
=671,
∴a2013=a3=-
;
点A1不能在y轴上(此时找不到B1),即x≠0,
点A1不能在x轴上(此时A2,在y轴上,找不到B2),即y=-x-1≠0,
解得:x≠-1;
综上可得a1不可取0、-1.
故答案为:-
、-
;0、-1.
| 1 |
| 2 |
B1的纵坐标和A2的纵坐标相同,则A2的横坐标为a2=-
| 3 |
| 2 |
A2的横坐标和B2的横坐标相同,则B2的纵坐标为b2=-
| 2 |
| 3 |

B2的纵坐标和A3的纵坐标相同,则A3的横坐标为a3=-
| 1 |
| 3 |
A3的横坐标和B3的横坐标相同,则B3的纵坐标为b3=-3,
B3的纵坐标和A4的纵坐标相同,则A4的横坐标为a4=2,
A4的横坐标和B4的横坐标相同,则B4的纵坐标为b4=
| 1 |
| 2 |
即当a1=2时,a2=-
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
b1=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
∵
| 2013 |
| 3 |
∴a2013=a3=-
| 1 |
| 3 |
点A1不能在y轴上(此时找不到B1),即x≠0,
点A1不能在x轴上(此时A2,在y轴上,找不到B2),即y=-x-1≠0,
解得:x≠-1;
综上可得a1不可取0、-1.
故答案为:-
| 3 |
| 2 |
| 1 |
| 3 |
点评:本题考查了反比例函数的综合,涉及了点的规律变化,解答此类题目一定要先计算出前面几个点的坐标,由特殊到一般进行规律的总结,难度较大.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
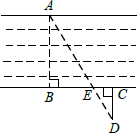 (2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
(2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )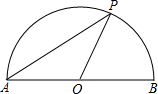 (2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) (2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
(2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=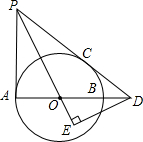 (2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.