题目内容
 (2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=
| 3 | 4 |
分析:(1)根据切线长定理和切线的性质即可证明:∠EPD=∠EDO;
(2)连接OC,利用tan∠PDA=
,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
(2)连接OC,利用tan∠PDA=
| 3 |
| 4 |
解答:(1)证明:PA,PC与⊙O分别相切于点A,C,
∴∠APO=∠EPD且PA⊥AO,
∴∠PAO=90°,
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO,
∴∠EPD=∠EDO;
(2)解:连接OC,
∴PA=PC=6,
∵tan∠PDA=
,
∴在Rt△PAD中,AD=8,PD=10,
∴CD=4,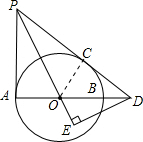
∵tan∠PDA=
,
∴在Rt△OCD中,OC=OA=3,OD=5,
∵∠EPD=∠ODE,
∴△OED∽△DEP,
∴
=
=
=2,
在Rt△OED中,OE2+DE2=52,
∴OE=
.
∴∠APO=∠EPD且PA⊥AO,
∴∠PAO=90°,
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO,
∴∠EPD=∠EDO;
(2)解:连接OC,
∴PA=PC=6,
∵tan∠PDA=
| 3 |
| 4 |
∴在Rt△PAD中,AD=8,PD=10,
∴CD=4,

∵tan∠PDA=
| 3 |
| 4 |
∴在Rt△OCD中,OC=OA=3,OD=5,
∵∠EPD=∠ODE,
∴△OED∽△DEP,
∴
| PD |
| DO |
| PE |
| DE |
| ED |
| OE |
在Rt△OED中,OE2+DE2=52,
∴OE=
| 5 |
点评:本题综合考查了切线长定理,相似三角形的性质和判定,勾股定理的应用,能综合运用性质进行推理和计算是解此题的关键,通过做此题培养了学生的分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
(2013•北京)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( ) (2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
(2013•北京)如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) (2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
(2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y= (2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
(2013•北京)如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=