Question

【题目】如图，Rt△ABC中，AB＝AC，∠BAC＝90°，点O是BC的中点，如果点M、N分别在线段AB、AC上移动，并在移动过程中始终保持AN＝BM．

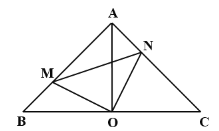
（1）求证：△ANO≌△BMO；

（2）求证：OM⊥ON．

Answer 1

【答案】(1)证明见解析;(2)证明见解析.

【解析】

（1）运用SAS即可证明△ANO≌△BMO；

（2）运用全等三角形的性质和垂直的定义证明即可；

证明：（1）∵AB=AC，∠BAC=90，O为BC的中点

∴OA⊥BC，OA=OB=OC，

∴∠NAO=∠B=45°，

在△AON和△BOM中

AN=BM ，∠NAO=∠B，OA=OB

∴△AON≌△BOM（SAS）；

（2）∵△AON≌△BOM

∴∠NOA=∠MOB

∵AO⊥BC，即∠AOB=90

∴∠MOB+∠AOM=90°

∴∠NOM=∠NOA+∠AOM=∠MOB+∠AOM=90°

∴OM⊥ON.