题目内容
 如图所示,在长方形ABCD中,AB=16,BC=8,将长方形沿AC折叠,使D落在点E处,且CE与AB交于点F,求AF的长.
如图所示,在长方形ABCD中,AB=16,BC=8,将长方形沿AC折叠,使D落在点E处,且CE与AB交于点F,求AF的长.分析:根据翻折的性质可得∠1=∠2,再根据两直线平行,内错角相等可得∠1=∠3,从而求出∠2=∠3,根据等角对等边可得AF=CF,设AF=CF=x,然后表示出BF,在Rt△BCF中,利用勾股定理列出方程求解即可.
解答: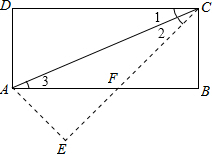 解:由翻折可得,∠1=∠2,
解:由翻折可得,∠1=∠2,
∵矩形ABCD的边CD∥AB,
∴∠1=∠3,
∴∠2=∠3,
∴AF=CF,
设AF=CF=x,
则BF=AB-AF=16-x,
在Rt△BCF中,BF2+BC2=CF2,
即(16-x)2+82=x2,
解得x=10,
即AF=10.
 解:由翻折可得,∠1=∠2,
解:由翻折可得,∠1=∠2,∵矩形ABCD的边CD∥AB,
∴∠1=∠3,
∴∠2=∠3,
∴AF=CF,
设AF=CF=x,
则BF=AB-AF=16-x,
在Rt△BCF中,BF2+BC2=CF2,
即(16-x)2+82=x2,
解得x=10,
即AF=10.
点评:本题考查了翻折变换的性质,勾股定理的应用,用AF表示出BF,然后根据勾股定理列出方程是解题的关键,也是本题的难点.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为( )
如图所示,在长方形ABCD中,E、F分别是AB、BC上的点,且BE=12,BF=16,则由点E到F的最短距离为( )| A、20 | B、24 | C、28 | D、32 |
 10、如图所示,在长方形ABCD的对称轴l上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有( )
10、如图所示,在长方形ABCD的对称轴l上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有( ) 如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置.
如图所示,在长方形ABCD中,AB=3,BC=9,将图形沿着EF对折,使得B点与D点重合,A点落在A′的位置. 如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?
如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?