题目内容
10、如图所示，在长方形ABCD的对称轴l上找点P，使得△PAB、△PBC均为等腰三角形，则满足条件的点P有（ ）分析：利用分类讨论的思想，此题共可找到5个符合条件的点：一是作AB或DC的垂直平分线交l于P；二是在长方形内部
在l上作点P，使PA=AB，PD=DC，同理，在l上作点P，使PC=DC，AB=PB；三是如图，在长方形外l上作点P，使AB=BP，DC=PC，同理，在长方形外l上作点P，使AP=AB，PD=DC．
在l上作点P，使PA=AB，PD=DC，同理，在l上作点P，使PC=DC，AB=PB；三是如图，在长方形外l上作点P，使AB=BP，DC=PC，同理，在长方形外l上作点P，使AP=AB，PD=DC．
解答：解：如图，作AB或DC的垂直平分线交l于P，
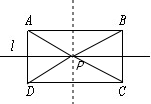
如图，在l上作点P，使PA=AB，PD=DC，
同理，在l上作点P，使PC=DC，AB=PB，
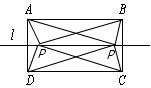
如图，在长方形外l上作点P，使AB=BP，DC=PC，
同理，在长方形外l上作点P，使AP=AB，PD=DC，
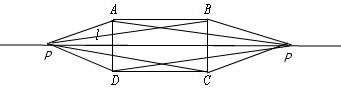
故答案为5．
如图，在l上作点P，使PA=AB，PD=DC，
同理，在l上作点P，使PC=DC，AB=PB，
如图，在长方形外l上作点P，使AB=BP，DC=PC，
同理，在长方形外l上作点P，使AP=AB，PD=DC，
故答案为5．
点评：本题考查了等腰三角形的判定；解题中利用等腰三角形的判定来解决特殊的实际问题，其关键是根据题意，结合图形，再利用数学知识来求解．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图所示，在长方形ABCD中，E、F分别是AB、BC上的点，且BE=12，BF=16，则由点E到F的最短距离为（ ）| A、20 | B、24 | C、28 | D、32 |
如图所示，在长方形ABCD中，AB=3，BC=9，将图形沿着EF对折，使得B点与D点重合，A点落在A′的位置．
如图所示，在长方形ABCD中，AB=16，BC=8，将长方形沿AC折叠，使D落在点E处，且CE与AB交于点F，求AF的长．
如图所示，在长方形ABCD中，AB=10cm，BC=6cm，试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2？