题目内容
【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于![]() EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=![]() DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=![]() S四边形ABCH.
S四边形ABCH.
其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
【答案】D
【解析】试题分析:①如图,连接EG,FG,
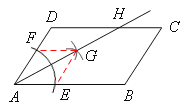
由作图可得,AE=AF,EG=FG,
又∵AG=AG,∴△AEG≌△AFG(SSS)。
∴∠EAG=∠FAG,即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中,DC∥AB,∴∠HAB=DHA。
由①∠HAB=∠HAD,∴∠HAD=DHA。∴DA=DH,即△ADH是等腰三角形。故结论③正确。
②若CH=![]() DH,由③可得AB=DC=
DH,由③可得AB=DC=![]() AD,与已知AB>CD条件不符。故结论②错误。
AD,与已知AB>CD条件不符。故结论②错误。
④若S△ADH=![]() S四边形ABCH,由③可得AB=DC=
S四边形ABCH,由③可得AB=DC=![]() AD,与已知AB>CD条件不符。故结论②错误。
AD,与已知AB>CD条件不符。故结论②错误。
综上所述,正确的有①③。故选D。

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从苏州出发,1日到4日在北京旅游,8月5日上午返回苏州.
苏州与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)他们往返都坐飞机 (成人票五五折),其他开支不变,至少要准备多少元?
(3)他们去时坐火车,回来坐飞机 (成人票五五折),其他开支不变,准备了14000元,是否够用?如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5﹣x |
|
|
(2)若要保证租车费用不超过1900元,求x的最大值.