题目内容
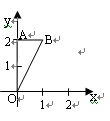
在平面直角坐标系中,点O为坐标原点,已知点A(0,1)、点B(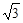 ,0),则∠OAB = ,点G为△ABO重心,则点G的坐标是 .
,0),则∠OAB = ,点G为△ABO重心,则点G的坐标是 .
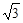 ,0),则∠OAB = ,点G为△ABO重心,则点G的坐标是 .
,0),则∠OAB = ,点G为△ABO重心,则点G的坐标是 .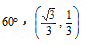
先根据题意画出图形,直接根据锐角三角函数的定义即可求出∠OAB的度数;再根据直角三角形的性质求出AB的长,进而得出AB的中线OD的长,由三角形重心的性质得出OG的长,再根据AB两点的坐标求出其中点D的坐标,利用待定系数法求出OD的解析式,设出G点坐标,利用两点间的距离公式即可得出G点坐标.
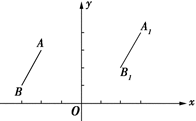
解答:解:如图所示:
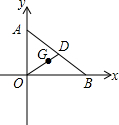
∵A(0,1),B(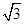 ,0),
,0),
∴OA=1,OB=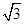 ,
,
∴tan∠OAB=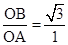 =
=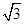 ,
,
∴∠OAB=60°;
∴∠ABO=30°,
∴AB=2OA=2,
∵点D为AB的中点,G为重心,
∴OD=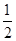 AB=
AB=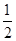 ×2=1,OG=
×2=1,OG=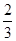 OD=
OD=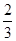 ×1=
×1=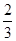 ,D(
,D(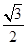 ,
,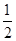 ),
),
设过O、D两点的直线解析式为y=kx,则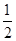 =
=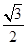 k,解得k=
k,解得k=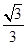 ,
,
∴过O、D两点的直线解析式为y=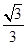 x,
x,
∴设G(x,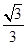 x),则OG=
x),则OG=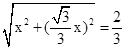 ,解得x=
,解得x=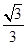 或x=-
或x=-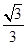 (舍去),
(舍去),
∴G(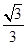 ,
,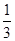 ).
).
故答案为:60°;(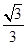 ,
,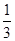 ).
).
解答:解:如图所示:

∵A(0,1),B(
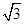 ,0),
,0),∴OA=1,OB=
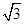 ,
,∴tan∠OAB=
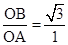 =
=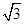 ,
,∴∠OAB=60°;
∴∠ABO=30°,
∴AB=2OA=2,
∵点D为AB的中点,G为重心,
∴OD=
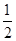 AB=
AB=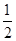 ×2=1,OG=
×2=1,OG=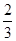 OD=
OD=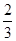 ×1=
×1=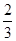 ,D(
,D(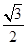 ,
,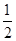 ),
),设过O、D两点的直线解析式为y=kx,则
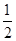 =
=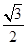 k,解得k=
k,解得k=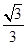 ,
,∴过O、D两点的直线解析式为y=
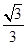 x,
x,∴设G(x,
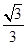 x),则OG=
x),则OG=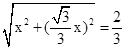 ,解得x=
,解得x=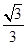 或x=-
或x=-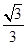 (舍去),
(舍去),∴G(
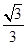 ,
,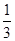 ).
).故答案为:60°;(
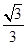 ,
,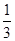 ).
).
练习册系列答案
相关题目
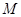 在
在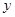 轴的左侧,到
轴的左侧,到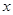 轴,
轴,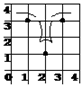
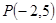 向左平移
向左平移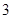 个单位,再向下平移
个单位,再向下平移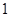 个单位后,所得的点的坐标是 .
个单位后,所得的点的坐标是 .