题目内容
证明题：
如图，已知AB=AD，AE=AC，∠DAC=∠BAE，
求证：DE=BC．
证明：∵∠DAC=∠BAE，
∴∠DAC+∠CAE=∠BAE+∠CAE，
即∠DAE=∠BAC，
∵在△DAE和△BAC中
，
∴△DAE≌△BAC，
∴DE=BC．
分析：求出∠DAE=∠BAC，根据SAS证△DAE≌△BAC，根据全等三角形的性质即可求出答案．
点评：本题考查了全等三角形的性质和判定的应用，主要考查学生运用性质进行推理的能力，题目比较典型，难度不大．
∴∠DAC+∠CAE=∠BAE+∠CAE，
即∠DAE=∠BAC，
∵在△DAE和△BAC中
，∴△DAE≌△BAC，
∴DE=BC．
分析：求出∠DAE=∠BAC，根据SAS证△DAE≌△BAC，根据全等三角形的性质即可求出答案．
点评：本题考查了全等三角形的性质和判定的应用，主要考查学生运用性质进行推理的能力，题目比较典型，难度不大．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
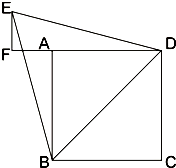的延长线的垂线EF，垂足为F．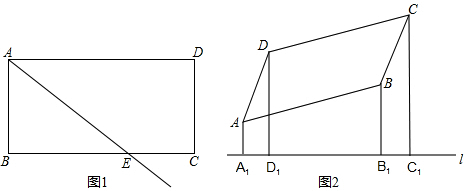
23、观察探索题：
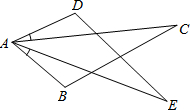证明题：