题目内容
在Rt△ABC中，斜边AB上的高CD=3cm，中线CE=4cm，则△ABC的面积等于________cm2．
12
分析：根据直角三角形斜边上中线的性质求出AB的长，根据三角形的面积公式求出即可．
解答：
解：∵CE是直角三角形ABC斜边上的中线，
∴AB=2CE=8cm，
∴△ABC的面积是
×AB×CD=×8×3=12（cm2）．
故答案为：12．
点评：本题主要考查对三角形的面积，直角三角形斜边上的中线的性质等知识点的理解和掌握，能求出AB的长是解此题的关键．
分析：根据直角三角形斜边上中线的性质求出AB的长，根据三角形的面积公式求出即可．
解答：
解：∵CE是直角三角形ABC斜边上的中线，∴AB=2CE=8cm，
∴△ABC的面积是
×AB×CD=×8×3=12（cm2）．故答案为：12．
点评：本题主要考查对三角形的面积，直角三角形斜边上的中线的性质等知识点的理解和掌握，能求出AB的长是解此题的关键．
练习册系列答案
相关题目
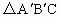的位置，其中
分别是A、B对应点，且点B在斜边
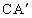交AB于D，这时∠BDC的度数是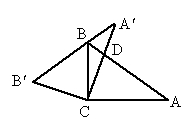
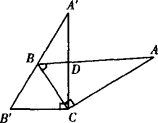
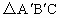的位置，使B在斜边
上，
C与AB相交于D，试确定∠BDC的度数．
的位置，其中
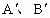分别是A、B对应点，且点B在斜边
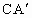交AB于D，这时∠BDC的度数是