题目内容
【题目】如图,直线l1∥l2 , l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
【答案】解:如图,过点A作AC⊥l2于点C,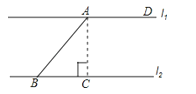
∵直线l1∥l2 , AC⊥l2 ,
∴∠DAC=90°,
∵∠DAB=135°,
∴∠BAC=∠DAB﹣∠DAC=45°,
∴∠ABC=45°,
∴∠BAC=∠ABC,
∴AC=BC,
在Rt△ABC中,AC2+BC2=AB2 ,
2AC2=502 ,
∴AC=25![]()
∴两平行线l1和l2之间的距离为25![]() .
.
【解析】过点A作AC⊥l2于点C,证明∠BAC=∠ABC,所以AC=BC,在Rt△ABC中,AC2+BC2=AB2 , 即可解答.
【考点精析】解答此题的关键在于理解平行线之间的距离的相关知识,掌握两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离.

练习册系列答案
相关题目