题目内容
【题目】如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是m2 . 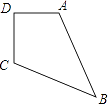
【答案】36
【解析】解:连接AC.
∵AD=3m,CD=4m,∠ADC=90°,
∴AC= ![]() =5m.
=5m.
∵BC=12m,AB=13m,
∴BC2+AC2=122+52=169(m2),AB2=132=169(m2),
∴BC2+AC2=AB2 ,
∴∠ACB=90°.
∴S四边形ABCD=SRt△ADC+SRt△ABC= ![]() ADDC+
ADDC+ ![]() ACAB=
ACAB= ![]() ×3×4+
×3×4+ ![]() ×12×5=36(m2).
×12×5=36(m2).
故这块地的面积为36m2 .
所以答案是36.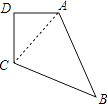
【考点精析】本题主要考查了勾股定理的概念和勾股定理的逆定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.

练习册系列答案
相关题目