题目内容
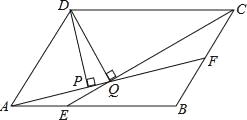
【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数![]() 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
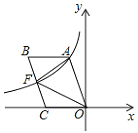
【答案】-16
【解析】∵△AOF的面积为12,四边形OABC是平行四边形,
∴△BOC的的面积是12,
∵F是BC的中点,
∴△FCO的面积是6,
设点A的坐标为(a, ![]() ),过点A作AM⊥x轴与点M,过点B作BP⊥x轴与点P,过点F作FN⊥x轴与点N,即可得△AOM≌△BCP,
),过点A作AM⊥x轴与点M,过点B作BP⊥x轴与点P,过点F作FN⊥x轴与点N,即可得△AOM≌△BCP,
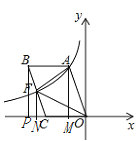
所以点P的纵坐标为![]() ,OM=PC=
,OM=PC= ![]() ,
,
∵F是BC的中点,
∴CN=![]() ,FN=
,FN=![]() .
.
∵点F在反比例函数的图象上,
∴![]() ,
,
解得x=2a.
即ON=![]() .
.
∴OC=![]() =
=![]() ,
,
∴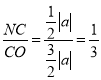 ,
,
∴![]() ,
,
∵△FCO的面积是6,
∴![]() ,
,
∴![]() ,
,
∵点F在第二象限,
所以k=-2×8=-16.
故答案为:-16.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目