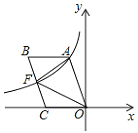
题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() 两点不重合),以
两点不重合),以![]() 为边作正方形
为边作正方形![]() ,使点
,使点![]() 与点
与点![]() 在直线
在直线![]() 的异侧,射线
的异侧,射线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图(1),判断:线段
上,如图(1),判断:线段![]() 与线段
与线段![]() 的数量关系: ,位置关系: .
的数量关系: ,位置关系: .
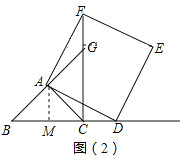
(2)如图(2),①若点![]() 在线段
在线段![]() 的延长线上,(1)中判断线段
的延长线上,(1)中判断线段![]() 与线段
与线段![]() 的数量关系与位置关系是否仍然成立,并说明理由;
的数量关系与位置关系是否仍然成立,并说明理由;
②当![]() 为
为![]() 中点,
中点,![]() 时,求线段
时,求线段![]() 的长.
的长.
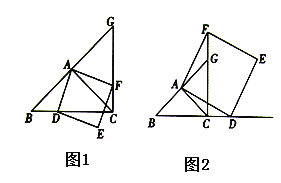
【答案】(1)数量关系:![]() ,位置关系:
,位置关系:![]() ;(2)①仍然成立,证明详见解析;②
;(2)①仍然成立,证明详见解析;② ![]()
【解析】
(1)根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;
(2)①根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;②如图(2),过点A作AM⊥BD于M,根据勾股定理可得AD=![]() .
.
(1)数量关系:![]() ,位置关系:
,位置关系:![]() ;
;
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
则在△BAD和△CAF中,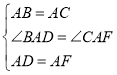 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠B=45°,BD=CF,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CG,
同理△ADC≌△AFG,
∴CD=GF,
∴BD+CD=CF+GF,
即BC=CG,
故答案为:BC=CG,BC⊥CG;
(2)①仍然成立
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
② 与①同理,可得BD=CF,BC=CG,BC⊥CG,
∵BC=2,G为CF中点,
∴CD=CG=FG=BC=2,
如图(2),过点A作AM⊥BD于M,
∴AM=1,MD=3,
∴AD=![]()