题目内容
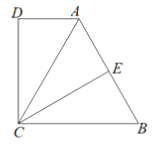
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC, AD=3,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,![]() AED的面积为6,则BC的长为_____.
AED的面积为6,则BC的长为_____.
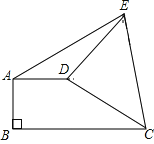
【答案】7
【解析】
过D作DM⊥BC于M,过E作EN⊥AD,交AD延长线于N,求出∠END=∠DMC,∠EDN=∠CDM,根据AAS证△EDN≌△CDM,求出EN=CM=4,即可求出答案.
过D作DM⊥BC于M,过E作EN⊥AD,交AD延长线于N,

∵AD=3,△ADE的面积为6,
∴![]() AD×EN=6,
AD×EN=6,
∴EN=4,
∵DM⊥BC,AD∥BC,
∴∠NDM=∠BMD=90°,
∵∠EDC=90°,
∴∠EDC-∠CDN=∠MDN-∠CDN,
∴∠EDN=∠CDM,
∵DM⊥BC,EN⊥AD,
∴∠END=∠DMC=90°,
在△END和△CMD中
 ,
,
∴△END≌△CMD(AAS),
∴EN=MC=4,
∵AB⊥BC,DM⊥BC,
∴DM∥AB,
∵AD∥BC,
∴四边形ABMD是平行四边形,
∴AD=BM=3,
∴BC=3+4=7,
故答案是:7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目