Question

【题目】已知等边△ABC中，点E是直线BC上一点，∠ADB=75°.

(1) 如图1，∠DAE=30°，证明：BE=DC；

(2) 如图2，点E在BC延长线上,CA平分∠DAE，求值

Answer 1

【答案】（1）见详解；（2） .

【解析】

（1）证△ABE≌△ACD即可得到BE=DC；

（2）利用含30°角的直角三角形三边关系求出CE的值，再通过△ABD∽△EBA求出BE的值，即可求得答案.

解：（1）∵∠ADB=75°

∴∠ADC=180°-75°=105°

∵∠AED+∠DAE=∠ADC，∠DAE=30°

∴∠AED=105°-30°=75°

∴∠AEB=105°=∠ADC

∵△ABC为等边三角形

∴AB=AC,∠B=∠C

在△ABE和△ACD中，

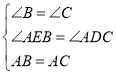
∴△ABE≌△ACD

∴BE=DC

（2）如图，过点A作AM⊥BC于M，

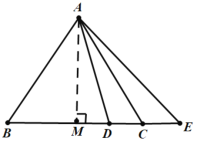
∵△ABC为等边三角形，∠ADB=75°

∴∠DAC=75°-60°=15°，

∵CA平分∠DAE，

∴∠CAE=15°，∠E=60°-15°=45°，

∴△AEM为等腰直角三角形

设AB=BC=AC=2a，

∵AM⊥BC，

易得BM=MC=a，AM=a，EM=a，

∴CE=，BE=2a+a-a=a+a，

在△ABD与△EBA中，∠ADB=∠BAE=75°，∠B=∠B，

∴△ABD∽△EBA，

∴,

∴

∴BD=2a-2a，

∴