题目内容
【题目】在矩形ABCD中,AB=1,AD= ![]() ,AF平分∠DAB , 过C点作CE⊥BD于E , 延长AF、EC交于点H , 下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED;正确的是( ).
,AF平分∠DAB , 过C点作CE⊥BD于E , 延长AF、EC交于点H , 下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED;正确的是( ).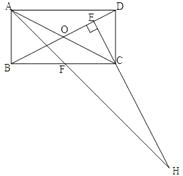
A.②③
B.③④
C.①②④
D.②③④
【答案】D
【解析】∵AB=1,AD= ![]() ,∴BD=AC=2,OB=OA=OD=OC=1,∴△OAB , △OCD为正三角形,∵AF平分∠DAB , ∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,∴BF=BO即②正确;∵AF平分∠DAB , ∴∠FAD=45°,∴∠CAH=45°-30°=15°,∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH即③正确;由正三角形上的高的性质可知:DE=OD÷2,OD=OB , ∴BE=3ED即④正确;若AF=FH , 那么点F为等腰三角形CAH的中点,那么CB垂直于AH , 显然不成立,①所以不正确.故选D.
,∴BD=AC=2,OB=OA=OD=OC=1,∴△OAB , △OCD为正三角形,∵AF平分∠DAB , ∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,∴BF=BO即②正确;∵AF平分∠DAB , ∴∠FAD=45°,∴∠CAH=45°-30°=15°,∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH即③正确;由正三角形上的高的性质可知:DE=OD÷2,OD=OB , ∴BE=3ED即④正确;若AF=FH , 那么点F为等腰三角形CAH的中点,那么CB垂直于AH , 显然不成立,①所以不正确.故选D.
【考点精析】本题主要考查了角平分线的性质定理和等腰三角形的性质的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目