题目内容
【题目】已知,如图,矩形ABCD的对角线AC , BD相交于点O , E , F分别是OA , OB的中点.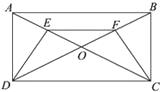
(1)求证:△ADE≌△BCF;
(2)若AD=4cm,AB=8cm,求OF的长.
【答案】
(1)
解答:证明:∵ABCD是矩形,
∴AD=BC,OA=OB,∠DAB=∠CAB=90°,
∴∠OAB=∠OBA,
∴∠DAB-∠OAB=∠CBA-∠OBA,即∠DAE=∠CBF,
∵E,F分别是OA,OB的中点,
∴AE= ![]() OA,BF=
OA,BF= ![]() OB,
OB,
∴AE=BF,
∴△ADE≌△BCF(SAS).
(2)
解答:解:在矩形ABCD中,AD=4cm,AB=8cm
∴BC=4cm,DC=8cm
∴BD= ![]() cm,
cm,
∴ ![]() cm,
cm,
又∵F是OB的中点,
∴OF= ![]() OB=
OB= ![]() cm.
cm.
【解析】矩形的两条对角线相等且平分.
【考点精析】掌握勾股定理的概念和矩形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目