题目内容
【题目】△ABC中,∠A=60°,点D、E分别是△ABC边AC、AB上的点(不与A、B、C重合),点P是一动点,令∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
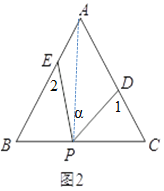
(1)若点P在边BC上,如图l,且∠α=50°,则∠1+∠2= °.
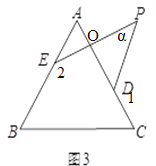
(2)若点P在边BC上运动,如图2,试判断∠α、∠1、∠2之间的关系,并证明.
(3)直接写出:若点P运动到△ABC形外,如图3,则∠α、∠l、∠2之间的关系为 .
【答案】(1)110°;(2)猜想:∠1+∠2=60°+∠![]() 证明见解析;(3)∠2-∠1+∠
证明见解析;(3)∠2-∠1+∠![]() =60°
=60°
【解析】试题分析:(1)连接PA,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PAD+∠APD,∠2=∠PAE+∠APE,再表示出∠1+∠2即可;(2)利用(1)中所求得出答案即可;(3)利用三角形内角和定理以及邻补角的性质可得出.
试题解析:
(1)如图,连接PC,
∵∠1=∠PAD+∠APD,∠2=∠PAE+∠APE,
∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A,
∵∠DPE=∠α=50°,∠A=60°,
∴∠1+∠2=50°+60°=110°
故答案为:110°;
(2)如图:连接PA,
∵∠1=∠PAD+∠APD,∠2=∠PAE+∠APE
∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A,
∵∠A=60°,∠DPE=∠α,
∴∠1+∠2=60°+∠α;
故答案为:∠1+∠2=60°+∠α;
(3)如图,
∵∠2=∠A+∠AOE,
∠1=∠α+∠POD;
∠AOE=∠POD
∴∠1∠2=∠A-∠α
即∠1∠2+∠α==60°

练习册系列答案
相关题目