��Ŀ����
��ƽ��ֱ������ϵ�У��ֽ�һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ�б����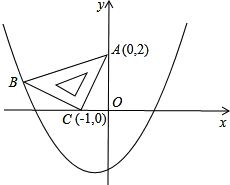 ���������ϣ��ҵ�A��0��2������C��-1��0������ͼ��ʾ��������y=ax2+ax-2������B��
���������ϣ��ҵ�A��0��2������C��-1��0������ͼ��ʾ��������y=ax2+ax-2������B����1�����B������������ߵĽ���ʽ��
��2����ABC��AC���е���ת180��õ���ABC�����жϵ�B�Ƿ����������ϣ���˵�����ɣ�
��3����G���������ϵĶ��㣬��x�����Ƿ���ڵ�P��ʹA��C��P��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��������1����B��x��Ĵ��ߣ��费��ΪD��ͨ��֤������BDC��������COAȫ�������B������ꣻ�ó�B�����������������ߵĽ���ʽ�м������a��ֵ��Ҳ��ȷ���������ߵĽ���ʽ��
��2�����ݣ�1����õ�B�������֪��B�����ú�AC���е����������ͬ�������������AC�е㣬ѡ��180���B��������겻�䣬�ɴ˿����B������Ϊ��2��1����������������ߵĽ���ʽ�м����ж�����ת��B���Ƿ����������ϣ�
��3���������������P��϶ࣺ
�ɽ�A�����������������ߵĽ���ʽ�У����������Q������꣬���ɵó�AQ�ij���Ȼ��C���������������ƽ��AQ����λ���ɵó�4������������P������ꣻȡA�����x��ĶԳƵ�A�䣬������������������ߵĽ���ʽ�У��ɵó���������������Q�����꣬Ȼ�����ֱ��AC��б�����ֱ��PQ�Ľ���ʽ�����ɵó�P������꣬��������ɵó�2������������P�����꣬��������Ӧ����6������������P�����꣮
��2�����ݣ�1����õ�B�������֪��B�����ú�AC���е����������ͬ�������������AC�е㣬ѡ��180���B��������겻�䣬�ɴ˿����B������Ϊ��2��1����������������ߵĽ���ʽ�м����ж�����ת��B���Ƿ����������ϣ�
��3���������������P��϶ࣺ
�ɽ�A�����������������ߵĽ���ʽ�У����������Q������꣬���ɵó�AQ�ij���Ȼ��C���������������ƽ��AQ����λ���ɵó�4������������P������ꣻȡA�����x��ĶԳƵ�A�䣬������������������ߵĽ���ʽ�У��ɵó���������������Q�����꣬Ȼ�����ֱ��AC��б�����ֱ��PQ�Ľ���ʽ�����ɵó�P������꣬��������ɵó�2������������P�����꣬��������Ӧ����6������������P�����꣮
����⣺��1������B��BD��x�ᣬ����ΪD��
�ߡ�BCD+��ACO=90�㣬��ACO+��OAC=90�㣻
���BCD=��CAO��
�֡ߡ�BDC=��COA=90�㣻CB=AC��
���BCD�ա�CAO��
��BD=OC=1��CD=OA=2��
���B��������-3��1����
��������y=ax2+ax-2������B��-3��1������õ�1=9a-3a-2��
���a=
��
���������߽���ʽΪy=
x2+
x-2��
��2��B��2��1��
�������B��2��1����������y=
x2+
x-2��
��3��P1��
��0����P2��
��0����P3��
��0����P4��
��0����P5��0��0����P6��1��0��
�ߡ�BCD+��ACO=90�㣬��ACO+��OAC=90�㣻
���BCD=��CAO��
�֡ߡ�BDC=��COA=90�㣻CB=AC��
���BCD�ա�CAO��
��BD=OC=1��CD=OA=2��
���B��������-3��1����
��������y=ax2+ax-2������B��-3��1������õ�1=9a-3a-2��
���a=
| 1 |
| 2 |
���������߽���ʽΪy=
| 1 |
| 2 |
| 1 |
| 2 |
��2��B��2��1��
�������B��2��1����������y=
| 1 |
| 2 |
| 1 |
| 2 |
��3��P1��
-1+
| ||
| 2 |
-1-
| ||
| 2 |
-3+
| ||
| 2 |
-3-
| ||
| 2 |
���������⿼���˵���ֱ�������ε����ʡ����κ�������ʽ��ȷ����ͼ�ε���ת������ͼ�㡢ƽ���ı��ε��ж���֪ʶ��Ҫע����ǣ�3������Ҫ�����п��ܵ����������ǵ�����Ҫ©�⣮

��ϰ��ϵ�д�
 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
�����Ŀ
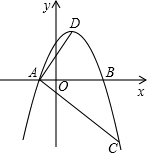 ����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=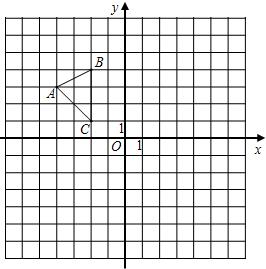 18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��
18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��