题目内容
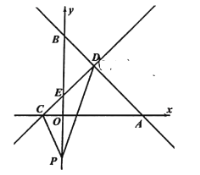
【题目】如图，将矩形
置于平面直角坐标系
中，
在
轴上，
在
轴上，点
的坐标为
，对角线
与
相交于点
，
是第一象限内一点．
（1）如图1，若
，
，试判断四边形
的形状，并说明理由；
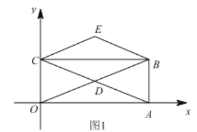
（2）如图2，当点使得
时，求证：
；
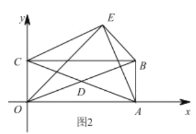
（3）在（2）的条件下，如果
与
恰好相等，求点的坐标．
【答案】（1）四边形BDCE是菱形，证明见解析 （2）证明见解析 （3）
【解析】
（1）根据
，
得证四边形BDCE是平行四边形，再根据矩形对角线的性质可得
，即可证明四边形BDCE是菱形；
（2）设
，根据两点间距离公式和勾股定理即可求证
；
（3）根据
与
恰好相等可得
，联立（2）中的方程
，即可解得x的值，再根据
是第一象限内一点，即可求出点的坐标．
（1）∵，
∴四边形BDCE是平行四边形
∵四边形ABCO是矩形
∴
∴四边形BDCE是菱形．
（2）设
∵四边形ABCO是矩形，点
的坐标为
∴
∴
，
，
∵
∴
∴
∴
，
，
∴
，
∴
∴．
（3）∵，，
∴
由（2）可得
将代入中
解得
将分别代入
中
，
∴
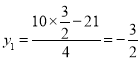或
∵是第一象限内一点
∴．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
