Question

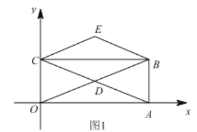
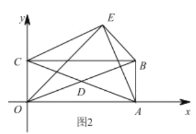
【题目】如图1，已知，，且，．

（1）求证：；

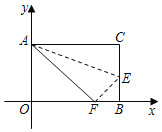
（2）如图2，若，，折叠纸片，使点与点重合，折痕为，且．

①求证：；

②点是线段上一点，连接，一动点从点出发，沿线段以每秒1个单位的速度运动到点，再沿线段以每秒个单位的速度运动到后停止，点在整个运动过程中用时最少多少秒？

Answer 1

【答案】（1）见详解；（2）①见详解；②.

【解析】

（1）直接利用AAS，即可证明结论成立；

（2）①由折叠的性质，得到BE=DE，EF平分∠BED，由DE⊥BC，得到∠DBE=∠ACB=∠FEB=45°，即可得到EF∥AC；

②当点Q是EF与BD的交点时，点在整个运动过程中用时最少；连接AQ、AD，可得△ADQ是等腰直角三角形，根据勾股定理求出BD，然后得到BQ=DQ=，然后求出AQ，即可求出点P运动所用的时间.

解：（1）由题意，

∵，，BC=CB，

∴（AAS）；

（2）①如图：

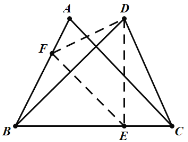
由折叠的性质，得到BE=DE，∠BEF=∠DEF，

∵DE⊥BC，

∴∠BED=90°，

∴∠BEF=∠DEF=∠DBE=∠BDE=45°；

∵，

∴∠ACB=∠DBE，

∴∠ACB=∠DBE=∠FEB=45°，

∴EF∥AC；

②如图，连接AQ交BC于点H，连接AD，当点Q是EF与BD的交点时，点在整个运动过程中用时最少；

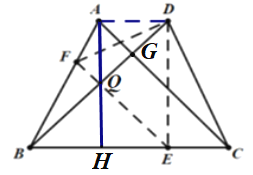
此时AQ∥DE，AD∥BC，

∴∠ADQ=45°，∠DAQ=90°，

∴△ADQ是等腰直角三角形，

∴AD=AQ，

∵点Q时BD中点，

∴点H是BE的中点，

∵BE=DE=，，

∴，

∴，，

∴点P运动所用的时间为：

（秒）.