Question

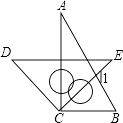
【题目】如图，△ABC中，AE是∠BAC的角平分线，AD是BC边上的高线，且∠B=50°，∠C=60°，则∠EAD的度数（ ）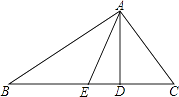
A.35°
B.5°
C.15°
D.25°

Answer 1

【答案】B
【解析】解：∵∠B=50°，∠C=60°， ∴∠BAC=180°﹣∠B﹣∠C=70°，
∵AE是∠BAC的角平分线，
∴∠EAC= ∠BAC=35°，
∵AD是高，
∴∠ADC=90°，
∴∠DAC=90°﹣∠C=30°，
∴∠EAD=∠EAC﹣∠DAC=5°．
故选B．
【考点精析】根据题目的已知条件，利用角的平分线和三角形的内角和外角的相关知识可以得到问题的答案，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．