题目内容
【题目】在矩形ABCD中,AB=4,AD=9点F是边BC上的一点,点E是AD上的一点,AE:ED=1:2,连接EF、DF,若EF=2![]() ,则CF的长为______________。
,则CF的长为______________。
【答案】8或4
【解析】
由题意先求出AE=3,ED=6,因为EF=2![]() >AB,分情况讨论点F在点E的左侧和右侧的情况,根据勾股定理求出GE(EH)即可求解.
>AB,分情况讨论点F在点E的左侧和右侧的情况,根据勾股定理求出GE(EH)即可求解.
解:∵AD=9,AE:ED=1:2,
∴AE=3,ED=6,
又∵EF=2![]() >AB,分情况讨论:
>AB,分情况讨论:
如下图:
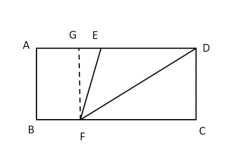
当点F在点E的左侧时,做FG垂直AD,则FCDG为矩形,AB=FG,
CF=GD=ED+GE,在RT三角形GFE中,GE=![]() =2,
=2,
则此时CF=6+2=8;
如下图:
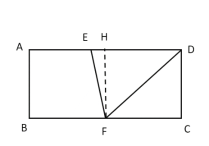
当点F在点E的右侧时,做FH垂直AD,同理可得CF=ED-EH,HF=AB=4,EH=2,
则此时CF=6-2=4;
综上,CF的长为8或4.

练习册系列答案
相关题目