题目内容
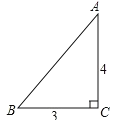
【题目】如图,一张三角形纸片ABC,其中![]() ,
,![]() ,
,![]() 现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处
现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处![]() 这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是
这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
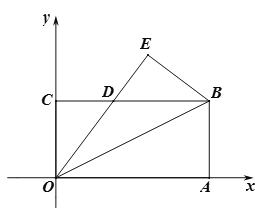
(1)图1,根据折叠得:DE是线段AC的垂直平分线,由中位线定理的推论可知:DE是△ABC的中位线,得出DE的长,即a的长;
(2)图2,同理可得:MN是△ABC的中位线,得出MN的长,即b的长;
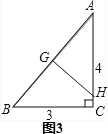
(3)图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.

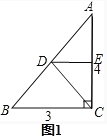 第一次折叠如图1,折痕为DE,
第一次折叠如图1,折痕为DE,
由折叠得:AE=EC=![]() AC=
AC=![]() ×4=2,DE⊥AC ,
×4=2,DE⊥AC ,
∵∠ACB=90°,
∴DE∥BC,
∴a=DE=![]() BC=
BC=![]() ×3=
×3=![]() ,
,
第二次折叠如图2,折痕为MN,
由折叠得:BN=NC=![]() BC=
BC=![]() ×3=
×3=![]() ,MN⊥BC.
,MN⊥BC.
∵∠ACB=90°,
∴MN∥AC,
∴b=MN=![]() AC=
AC=![]() ×4=2,
×4=2,
第三次折叠如图3,折痕为GH,
由勾股定理得:AB=![]() =5,
=5,
由折叠得:AG=BG=![]() AB=
AB=![]() ×5=
×5=![]() ,GH⊥AB,
,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠ACB,
∴△ACB∽△AGH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴GH=![]() ,即c=
,即c=![]() ,
,
∵2>![]() ,>
,>![]() ,
,
∴b>c>a.
故答案为:D.

【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)