题目内容
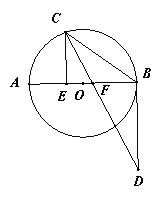
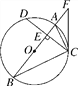
【题目】如图,在⊙O中,直径AB⊥弦CD于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.
(1)求证:CF是⊙O的切线;
(2)若AE=4,tan∠ACD=![]() ,求FC的长.
,求FC的长.
【答案】(1)见解析
【解析】分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案;
(2)根据正切的性质求出EC的长,然后利用垂径定理求出圆的半径,再根据等边三角形的性质,利用勾股定理求出即可.
详解:(1)证明:连接OC.∵AB是⊙O的直径,
∴∠ACB=90°,∴∠OCB+∠ACO=90°.
∵OB=OC,∴∠B=∠OCB.
又∵∠FCA=∠B,∴∠FCA=∠OCB,
∴∠FCA+∠ACO=90°,即∠FCO=90°,
∴FC⊥OC,
∴FC是⊙O切线.
(2)解:∵AB⊥CD,∴∠AEC=90°,∴EC=![]() ,
,
设OA=OC=r,则OE=OA-AE=r-4.
在Rt△OEC中,OC2=OE2+CE2,
即r2=(r-4)2+(4![]() )2,解得r=8.
)2,解得r=8.
∴OE=r-4=4=AE.
∵CE⊥OA,∴CA=CO=8,
∴△AOC是等边三角形,
∴∠FOC=60°,∴∠F=30°.
在Rt△FOC中,
∵∠OCF=90°,OC=8,∠F=30°,
∴OF=2OC=16,
∴FC=![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 75 | |
乙 | 78 | 80.5 |
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).