题目内容
 如图,已知在平行四边形ABCD中,E为AD的中点,CE的延长线交BA的延长于点F.
如图,已知在平行四边形ABCD中,E为AD的中点,CE的延长线交BA的延长于点F.
(1)求证:CD=FA;
(2)若∠B=∠F,连接AC、DF,所得到的四边形AFDC是什么四边形?
(3)若使∠F=∠BCF,平行四边形ABCD的边长之间还需要添加一个什么条件?请你补上这个条件,并进行证明(不要添加辅助线)
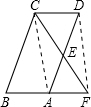 (1)证明:平行四边形ABCD中,CD∥BA,
(1)证明:平行四边形ABCD中,CD∥BA,∵点F在线段BA的延长线上,
∴CD∥BF,
∴∠CDE=∠FAE.
又∵E为AD的中点,
∴DE=AE.
在△CDE和△FAE中,
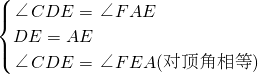 ,
,∴△CDE≌△FAE(ASA),
∴CD=FA(全等三角形的对应边相等);
(2)四边形AFDC是矩形.理由如下:
由(1)知,CD=FA.CD∥AF,则四边形AFDC是平行四边形.
∵∠B=∠BFC,
∴BC=FC.
又∵BC=AD,
∴FC=AD,
∴平行四边形AFDC是矩形;
(3)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB,
证明:∵由(1)知,△CED≌△FEA,
∴CD=AF.
又∵四边形ABCD是平行四边形,
∴CD=AB.
∴AB=AF,即BF=2AB.
∵BC=2AB.
∵BF=BC,
∴∠F=∠BCF.
分析:(1)通过全等三角形:△CDE≌△FAE,的对应边相等证得结论;
(2)四边形AFDC是矩形.由平行四边形ABCD的对边BC=AD、等腰△BCF的两腰BC=CF,则四边形AFDC的对角线CF=AD;
(3)由(1)易证得BF=2AB,可得当BC=2AB时,即BC=BF时,∠F=∠BCF.
点评:此题考查了平行四边形的性质、等腰三角形的性质以及全等三角形的判定与性质.此题难度适中,解题的关键是注意掌握数形结合思想的应用.

练习册系列答案
相关题目

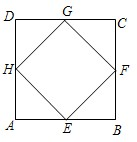 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.


