��Ŀ����
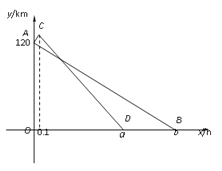
����Ŀ������������10�֣���M�ص�N����һ����ͨ��·����·��Ϊ120km����һ�����ٹ�·����·��Ϊ126km���׳����ҳ�ͬʱ��M�ؿ���N�أ��׳�ȫ������ͨ��·���ҳ�����ʻ����һ����ͨ��·��Ȼ�����ϸ��ٹ�·��������������ͨ��·���ٹ�·�Ϸֱ𱣳�������ʻ����������ͨ��·�ϵ��г��ٶ�Ϊ60km/h���ڸ��ٹ�·�ϵ��г��ٶ�Ϊ100km/h������������x hʱ����N�ص�·��Ϊy km��ͼ�е��߶�AB������ACD�ֱ��ʾ�׳����ҳ���y��x֮��ĺ�����ϵ��
��1����գ�a�� ��b�� ��
��2�����߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3�������ں�ʱ�������N�ص�·��֮��ﵽ��30km��
���𰸡���1��1.36��2����2��y1=��60x+120��y2=��100x+136��
��3����1.15��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
�������������������1�����C���꣬�ٸ���ʱ��=·�����ٶȷֱ�����׳�����ͨ��·����ʻ��ʱ�估�ҳ��ڸ��ٹ�·����ʻ��ʱ�䣬�ɵ�a��b��ֵ��
��2������A��B��C��D�ĵ��������ϵ�������ɵ��߶�AB��CD����ʾ��y��x֮��ĺ�����ϵʽ��
��3���������ۣ���0��x��0.1ʱ���ɽ���ʽ��֪�ס���������������Ϊ12����0.1��x��1.36ʱ����y1��y2��30�в���ʽ�ɵ�x�ķ�Χ����1.36��x��2ʱ����y1��30�в���ʽ�ɵô�ʱx�ķ�Χ���ۺ�������������ɵô𰸣�
�����������1���������⣬֪����C������Ϊ��0.1��126����
��a=0.1+![]() =1.36��b=
=1.36��b=![]() =2��
=2��
�ʴ�Ϊ��1.36��2��
��2�����߶�AB����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy1=k1x+b1��
��A��0��120����B��2��0�����������ã�
![]() ��
��
��ã� ![]() ��
��
��y1=��60x+120��
���߶�CD����ʾ��y��x֮��ĺ�����ϵʽ�ֱ�Ϊy2=k2x+b2��
��C��0.1��126����D��1.36��0�����������ã�
![]() ��
��
��ã� ![]() ��
��
��y2=��100x+136��
��3�������⣬����x=0.1ʱ��������N�ص�·��֮����12km��
����0��x��0.1ʱ��������N�ص�·��֮����ܴﵽ��30km��
����0.1��x��1.36ʱ����y1��y2��30���ã���60x+120��������100x+136����30��
���x��1.15��
����1.15��x��1.36ʱ��������N�ص�·��֮��ﵽ��30km��
����1.36��x��2ʱ����y1��30������60x+120��30�����x��1.5��
����1.36��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��
���ϣ���1.15��x��1.5ʱ��������N�ص�·��֮��ﵽ��30km��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�