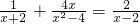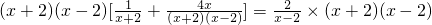题目内容

阅读下列解方程的过程，并填空
【题目】解方程

x+2

x2-4

x-2

[解]方程两边同时乘以（x+2）（x-2）…（A）(x+2)(x-2)[

x+2

(x+2)(x-2)

x-2

×(x+2)(x-2)
化简得：x-2+4x=2（x+2）…．…．（B）
去括号、移项得：x+4x-2x=4+2…（C）
解得：x=2 …（D）
∴原方程的解是x=2 …（E）
【问题】①上述解题过程的错误在第

步，其原因是

②该步改正为：

分析：通过阅读解题过程发现，解题过程的错误在最后一步即E步，原因是没有经过检验，即没有把求出的x=2代入最简公分母进行计算，看是否为0，事实上把x=2代入最简公分母（x+2）（x-2）计算后，其值为0，说明x=2是增根，原分式方程无解．

解答：解：上述解题过程的错误在第E步，其原因是没有进行检验，
该步改正为：把x=2代入（x+2）（x-2）得：（2+2）（2-2）=0，
∴x=2是增根，原方程无解．
故答案为：E；没有进行检验．

点评：此题考查了分式方程的解法，解分式方程的基本思路是转换，即把分式方程转换为整式方程，利用整式方程的解法来求解，而转换的关键是找出各分母的最简公分母，利用去分母的方法转“分”为“整”，最后求出方程的解后，必须检验求出的x是否满足分式方程，其方法是把求出的x的值代入最简公分母中进行计算，看其值是否为0，若为0，求出的x为分式方程的增根，若不为0，求出的x的值即为分式方程的解．

练习册系列答案

相关题目

先阅读下列解方程的过程，然后回答问题.

解：将原方程整理为(第一步)；方程两边都除以(x－1)，得(第二步)；去分母，得2(x＋1)＋2x＝5x(第三步)，解这个整式方程得x＝2(第四步).上面的解题过程中，

(1)

出现错误的一步是________

(2)

方程的正确解应是________

(3)

上述解题过程还缺少的一步是________

阅读下列解方程的过程，然后完成后面的习题。

解方程。

解：去分母，得。

去括号，得。

移项，得。

合并同类项，得5x＝4

∴。

（1）解方程过程中共出现　　　　　　　处错误，分别是第　　　　　　　步；

（2）写出正确的求解过程。

阅读下列解方程的过程，然后回答问题．

解方程．

解：(第一步)设y＝，则原方程可以化为y²－5y＋6＝0．

(第二步)解这个方程得y₁＝2，y₂＝3．

(第三步)当y₁＝2时，即＝2，解得x₁＝2．

当y₂＝3时，即＝3，解得

(第四步)所以原方程的根为x₁＝2，．

问题：

(1)

在第一步中，使用的方法是________．

(2)

在第二步中，解此一元二次方程用哪一种方法最为简捷？从下面选项中选择一种是
[　　]
A．	公式法
B．	配方法
C．	因式分解法
D．	直接开平方法

(3)

上述解题过程是否完整，若不完整，请补充．

(4)

上述解题过程中用到了
[　　]
A．	数形结合思想
B．	转化思想
C．	整体思想
D．	函数思想
E．	统计思想

阅读下列解方程的过程，并填空
【题目】解方程 $数学公式$
[解]方程两边同时乘以（x+2）（x-2）…（A） $数学公式$
化简得：x-2+4x=2（x+2）…．…．（B）
去括号、移项得：x+4x-2x=4+2…（C）
解得：x=2　　…（D）
∴原方程的解是x=2　 …（E）
【问题】①上述解题过程的错误在第步，其原因是②该步改正为：

试题分类