题目内容
 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
解:连接AC、BD,AC与BD相交于点M,过点M作ME⊥x轴于点E,过点C作CF⊥x轴于点F,

∵C(10,4),
∴AF=10,CF=4,
∵四边形ABCD为平行四边形,
∴AM=CM,即 =
= ,
,
∵ME⊥x轴,CF⊥x轴,
∴∠MEA=∠CFA=90°,
∴ME∥CF,
∴∠AME=∠ACF,∠AEM=∠AFC,
∴△AME∽△ACF,
∴ =
= =
= ,即E为AF的中点,
,即E为AF的中点,
∴ME为△AFC的中位线,…
∴AE= AF=5,ME=
AF=5,ME= CF=2,
CF=2,
∴M(5,2),
∵直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,
∴直线y=ax-2a-1经过点M,
将M(5,2)代入y=ax-2a-1得:a=1.
分析:连接AC、BD,AC与BD相交于点M,过点M作ME⊥x轴于点E,过点C作CF⊥x轴于点F,由直线将平行四边形分成面积相等的两部分,得到此直线过平行四边形对角线的交点M,接下来求M的坐标,由平行四边形的对角线互相平分,得到M为AC的中点,再由ME与CF都与x轴垂直,得到ME与CF平行,可得出两对同位角相等,根据两对对应角相等的两三角形相似,可得三角形AME与三角形ACF相似,由M为AC的中点得到相似三角形的相似比为1:2,可得E为AF的中点,由C的坐标得到AF与CF的长,又ME为三角形ACF的中位线,根据中位线定理得到ME为CF的一半,求出ME的长,由AE为AF的一半,求出AE的长,确定出M的坐标,把M的坐标代入直线方程中,得到关于a的方程,求出方程的解即可得到a的值.
点评:此题属于一次函数的综合题,涉及的知识有:平行四边形的性质,相似三角形的判定与性质,平行线的性质,三角形中位线定理,其中根据题意得出直线过平行四边形的中心M是解本题的关键.

∵C(10,4),
∴AF=10,CF=4,
∵四边形ABCD为平行四边形,
∴AM=CM,即
 =
= ,
,∵ME⊥x轴,CF⊥x轴,
∴∠MEA=∠CFA=90°,
∴ME∥CF,
∴∠AME=∠ACF,∠AEM=∠AFC,
∴△AME∽△ACF,
∴
 =
= =
= ,即E为AF的中点,
,即E为AF的中点,∴ME为△AFC的中位线,…
∴AE=
 AF=5,ME=
AF=5,ME= CF=2,
CF=2,∴M(5,2),
∵直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,
∴直线y=ax-2a-1经过点M,
将M(5,2)代入y=ax-2a-1得:a=1.
分析:连接AC、BD,AC与BD相交于点M,过点M作ME⊥x轴于点E,过点C作CF⊥x轴于点F,由直线将平行四边形分成面积相等的两部分,得到此直线过平行四边形对角线的交点M,接下来求M的坐标,由平行四边形的对角线互相平分,得到M为AC的中点,再由ME与CF都与x轴垂直,得到ME与CF平行,可得出两对同位角相等,根据两对对应角相等的两三角形相似,可得三角形AME与三角形ACF相似,由M为AC的中点得到相似三角形的相似比为1:2,可得E为AF的中点,由C的坐标得到AF与CF的长,又ME为三角形ACF的中位线,根据中位线定理得到ME为CF的一半,求出ME的长,由AE为AF的一半,求出AE的长,确定出M的坐标,把M的坐标代入直线方程中,得到关于a的方程,求出方程的解即可得到a的值.
点评:此题属于一次函数的综合题,涉及的知识有:平行四边形的性质,相似三角形的判定与性质,平行线的性质,三角形中位线定理,其中根据题意得出直线过平行四边形的中心M是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
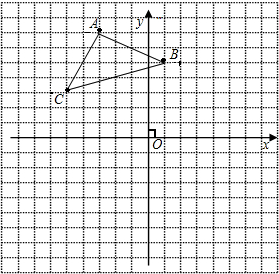 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),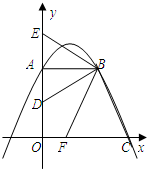 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
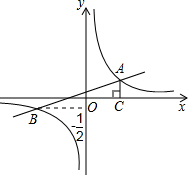 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示