��Ŀ����
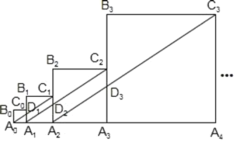
����Ŀ�����壺��ƽ���ı����У�����һ���Խ�����һ�ߵ�������������ƽ���ı���Ϊ�����ı��Σ����������Խ��߽��������Խ��ߣ������߽��������ߣ�
��ͼ1���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
�� ![]() ��
��
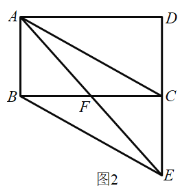
��1����![]() ����ͼ2��
����ͼ2��
�ٵ�![]() ʱ����˵���ı���
ʱ����˵���ı���![]() �������ı��Σ�
�������ı��Σ�
���Ƿ����ֵ![]() ��ʹ���ı���
��ʹ���ı���![]() �������ı��Σ������ڣ����
�������ı��Σ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
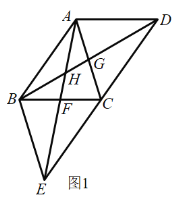
��2����ͼ1���ı���![]() ���ı���
���ı���![]() ���������ı��Σ�����
���������ı��Σ�����![]() ��
��![]() Ϊ�����Խ��ߣ�
Ϊ�����Խ��ߣ�![]() ��
��![]() Ϊ�����ߣ���
Ϊ�����ߣ���![]() ��ֵ��
��ֵ��
���𰸡���1����֤�����������ڴ��ڣ�![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ����2��
����2��![]() ��
��
��������
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�![]() �����ɵõ����ۣ�
�����ɵõ����ۣ�
�ڵ�AC=2CDʱ���ı���ABCD�������ı��Σ���ʱ AD=BC=![]() ����AC=2ADʱ���ı���ABCD�������ı��Σ��ɹ��ɶ����ó�����m2+12=��2m��2���ⷽ�̼��ɣ�
����AC=2ADʱ���ı���ABCD�������ı��Σ��ɹ��ɶ����ó�����m2+12=��2m��2���ⷽ�̼��ɣ�
��2���������ı��εĶ���ó�AD=DG���ó���DAG=��AGD��ͬ��AC=AF���ó���ACF=��AFC��֤����ADG=��CAF��![]() ���ó���ADB�ס�ACE����AB=CE���ó���ADB�ա�ACE����ȫ�������ε����ʵó�AC=AD����DM��AC��M����AM=x����AC=AD=4x���ɹ��ɶ����ã�DM=
���ó���ADB�ס�ACE����AB=CE���ó���ADB�ա�ACE����ȫ�������ε����ʵó�AC=AD����DM��AC��M����AM=x����AC=AD=4x���ɹ��ɶ����ã�DM=![]() ��CD=
��CD=![]() ����CD=AB=1�ó����̣��ⷽ�̼�����
����CD=AB=1�ó����̣��ⷽ�̼�����
��1����֤�������ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��AB��CD��BC=AD=2��
��![]() ��AB��CE��
��AB��CE��
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�![]() ��
��
![]() �ı���
�ı���![]() �������ı��Σ�
�������ı��Σ�
�ڴ��ڣ��������£�
��AC=2ABʱ����AC=2��
��![]() ��
��
��![]() ,
,
��m=AD=BC=![]() ��
��
��AC=2ADʱ����AC=2m��
��![]() ��
��
���m=![]() ��m=-
��m=-![]() ����ȥ����
����ȥ����
��![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ʱ���ı���
ʱ���ı���![]() �������ı��Σ�
�������ı��Σ�
��2�����ı���ABCD�������ı��Σ�BDΪ�����Խ��ߣ�ADΪ�����ߣ�
��AD=DG��
���DAG=��AGD��
���ı���ABEC�������ı��Σ�AEΪ�����Խ��ߣ�ACΪ�����ߣ�
��AC=AF��
���ACF=��AFC��
�֡ߡ�DAG=��ACF��
���DAG=��AGD=��ACF=��AFC��
���ADG=��CAF��
�֡�![]() ��
��![]() ��
��
��![]() ��
��
���ADB�ס�ACE��
�֡�AB=CE��
�����Ʊ�Ϊ1��
���ADB�ա�ACE��
��AC=AD��
��DM��AC��M����ͼ1��
��AM=x����AC=AD=4x��
��Rt��ADM�У��ɹ��ɶ����ã�DM=![]() ��
��
��Rt��DMC�У��ɹ��ɶ����ã�CD=![]() ��
��
��CD=AB=1��
�� ![]() =1��
=1��
��x=![]() ��
��
��AD=4x=![]() ��
��
��![]() ��
��


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�����Ŀ�����ҽ����������ÿ�����һСʱ������������ʮ�꣬�Ҹ�����һ������.������ij��ѧ�Ծ��꼶����ѧ�������ʾ�����������ϲ���Ķ�����Ŀ��ʲô�������涨���������������ܲ���������Ӿ�������������������������ѡ����ѡ���Լ���ϲ������Ŀ����ֻ��ѡ��һ����Ŀ���������������Ƴ�����������������ͳ��ͼ.
��ϲ���Ķ�����Ŀ | ���� |
���� | 120 |
�ܲ� |
|
��Ӿ |
|
���� | 30 |
���� |
|
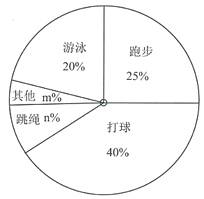
��1������ʾ������ѧ��������Ϊ ������![]() ��
��
��2������ͳ��ͼ�У�![]() ������������Ӧ�����ε�Բ�ĽǵĶ���Ϊ �ȣ�
������������Ӧ�����ε�Բ�ĽǵĶ���Ϊ �ȣ�
��3�������꼶��1200��ѧ��������ϲ������������Ŀ��ѧ����Լ�ж����ˣ�