题目内容
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+C与x轴交于点A(﹣1,0),B(﹣3,0),与y轴交于点C,顶点为D,抛物线的对称轴与x轴的交点为E.
(1)求抛物线的解析式及E点的坐标;
(2)设点P是抛物线对称轴上一点,且∠BPD=∠BCA,求点P的坐标;
(3)点F的坐标为(﹣2,4),若点Q在该抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线OF相切,求点Q的坐标.

【答案】(1)(﹣2,0);(2)(﹣2,2)或(﹣2,﹣2);(3)(﹣2, ![]() )或(﹣2,
)或(﹣2,![]() )
)
【解析】
(1)根据抛物线y=﹣x2+bx+C与x轴交于点A(﹣1,0),B(﹣3,0),利用待定系数法即可求得抛物线的解析式,配方后即可求得点E的坐标;
(2)根据点P是抛物线对称轴上一点,且∠BPD=∠BCA,分情况结合三角函数的知识进行求解即可求得点P的坐标;
(3)根据题意可知点Q到点A的距离,从而可以得到点Q到直线OF的距离,然后根据锐角三角函数即可求得点Q的坐标,从而可以解答本题.
(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(﹣3,0),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为y=﹣x2﹣4x﹣3,
∵y=﹣x2﹣4x﹣3=﹣(x+2)2+1,
∴点E的坐标为(﹣2,0);
(2)如图1所示,
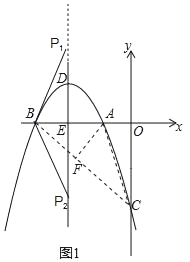
∵y=﹣x2﹣4x﹣3,点A(﹣1,0),B(﹣3,0),
∴点C(0,﹣3),
∴AB=(﹣1)﹣(﹣3)=2,AC=![]() ,OC=3,BC=3
,OC=3,BC=3![]() ,
,
作AF⊥BC于点F,
则![]() ,
,
即![]() ,
,
解得,AF=![]() ,
,
∴BF=![]() ,
,
∴CF=2![]() ,
,
∴tan∠ACB=![]() ,
,
设点P1的坐标为(﹣2,p),
∵∠BPD=∠BCA,
∴tan∠BPD=![]() ,
,
∵BE=1,
∴![]() ,
,
解得,P1E=2,
∴点P1的坐标为(﹣2,2),
同理可得,点P2的坐标为(﹣2,﹣2),
即点P的坐标为(﹣2,2)或(﹣2,﹣2);
(3)设过点O(0,0)和点F(﹣2,4)的直线的解析式为y=kx,
4=﹣2k,得k=﹣2,
∴直线OF的解析式为y=﹣2x,
当Q1在x轴上方时,设点Q1的坐标为(﹣2,t),如图2所示,
∵以Q为圆心的圆过A、B两点,并且和直线OF相切,
∴Q1A=![]() ,tan∠F=
,tan∠F=![]() ,
,
∴sin∠F=![]() ,
,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得,t=![]() 或t=
或t=![]() (舍去),
(舍去),
同理可得,当Q2在x轴下方的位置时,t=![]() ,
,
∴点Q的坐标为(﹣2,![]() )或(﹣2,
)或(﹣2,![]() ).
).