题目内容
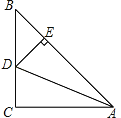
【题目】如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是6，则AB= ，AC= ．
【答案】6；3
【解析】
试题根据角平分线上的点到角的两边距离相等可得CD=DE，再判断出△BDE是等腰直角三角形，设BE=x，然后根据△BDE的周长列方程求出x的值，再分别求解即可．
解：∵∠C=90°，AD平分∠BAC交BC于点D，DE⊥AB，
∴CD=DE，
∵AC=BC，
∴∠B=45°，
∴△BDE是等腰直角三角形，
设BE=x，则CD=DE=x，BD=
x，
∵△BDE的周长是6，
∴x+x+x=6，
解得x=6﹣3，
∴AC=BC=x+x=6﹣3+（6﹣3）=3，
AB=AC=×3=6．
故答案为：6；3．
练习册系列答案
中考解读考点精练系列答案
相关题目
