题目内容
在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,若要使△ABC≌△A′B′C′,还要从下列条件中选取一个,则不符合的条件是
- A.∠A=∠A′
- B.∠C=∠C′
- C.BC=B′C′
- D.AC=A′C′
D
分析:要正确选出答案,要看现有的已知条件:一边,一角对应相等,添加任意一角都能证得全等,而添加一边若是已知角的对边,则满足SSA是不能证得三角形全等的,于是可得答案.
解答:A、∠A=∠A′符合ASA,能判定;
B、∠C=∠C′符合AAS,能判定;
C、BC=B′C′符合SAS,能判定;
D、AC=A′C′满足SSA,不能判定.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.此题是一道开放性题,实则还是考查学生对三角形全等的判定方法的掌握情况.此处可以运用排除法进行分析.
分析:要正确选出答案,要看现有的已知条件:一边,一角对应相等,添加任意一角都能证得全等,而添加一边若是已知角的对边,则满足SSA是不能证得三角形全等的,于是可得答案.
解答:A、∠A=∠A′符合ASA,能判定;
B、∠C=∠C′符合AAS,能判定;
C、BC=B′C′符合SAS,能判定;
D、AC=A′C′满足SSA,不能判定.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.此题是一道开放性题,实则还是考查学生对三角形全等的判定方法的掌握情况.此处可以运用排除法进行分析.

练习册系列答案
相关题目
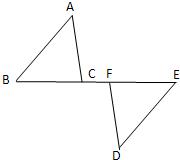 17、如图,在△ABC和△DEF中,AB=DE,当
17、如图,在△ABC和△DEF中,AB=DE,当 16、完成下面的证明过程:
16、完成下面的证明过程: 29、如图,在△ABC和△ADE中,AB=AD,AC=AE,∠DAC=∠BAE.
29、如图,在△ABC和△ADE中,AB=AD,AC=AE,∠DAC=∠BAE. 根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.
根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.