Question

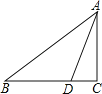
【题目】如图，Rt△ABC中，∠C=90°，BD=4，CD=2，∠ADB=3∠ABD，则AD= ．

Answer 1

【答案】．

【解析】

试题分析：如图，作BD的垂直平分线，交AB于点E，连接DE，设∠ABD=α，证明∠AED=∠ADE=2α，AE=AD；证明AE=2BE（设为2λ），得到AD=AE=2λ；利用勾股定理，可证明4λ2﹣4=9λ2﹣36，解得：λ=，求出AD即可解决问题．

解：如图，作BD的垂直平分线，交AB于点E，连接DE，设∠ABD=α，设BE=λ，

则BE=DE=λ，BF=DF=2，CF=4；

∴∠ABD=∠EDB=α；

∵∠AED=∠ABD+∠EDB=2α，∠ADB=3∠ABD=3α，

∴∠AED=∠ADE=2α，AE=AD；

∵EF⊥BC，AC⊥BC，

∴EF∥AC，==2，

∴AE=2BE=2λ，

∴AD=AE=2λ；

由勾股定理得：

AC2=AD2﹣DC2=4λ2﹣4，

AC2=AB2﹣BC2=9λ2﹣36，

∴4λ2﹣4=9λ2﹣36，

解得：λ=，

∴AD=，

故答案为：．