题目内容
【题目】如图，E是矩形ABCD的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H。
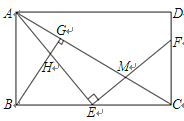
（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长。
【答案】（1）证明见解析；（2）
，证明见解析；（3）
【解析】
试题分析：（1）由四边形ABCD是矩形，可得
由
，利用同角的余角相等，可得
，然后利用有两组角对应相等的两个三角形相似，即可证得：
；
由
，易证得
，又由（1）中
，即可证得
；
首先作
，垂足为R，由
，即可求得MR的长，又由
，即可求得答案.
试题解析：（1）
四边形ABCD是矩形，
，
；
（2）.理由：
由（1）知
，
；
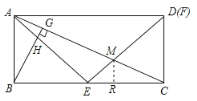
（3）如图所示，作
，垂足为R，由
,
在
中，
练习册系列答案
名校课堂系列答案
相关题目
